Giải chi tiết Câu hỏi Hoạt động 3 trang 17 SGK Toán 12 Cánh diều – Bài 2. Tính đơn điệu của hàm số.
Câu hỏi/Đề bài:
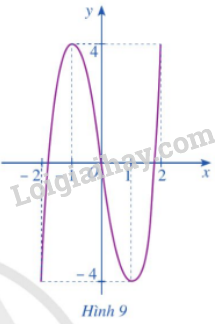
Cho hàm số \(y = f\left( x \right) = 2{x^3} – 6x,x \in \left[ { – 2;2} \right]\) có đồ thị là đường cong ở Hình 9.
a) Dựa vào đồ thị ở Hình 9, hãy cho biết các giá trị \(M = \mathop {\max }\limits_{\left[ { – 2;2} \right]} f\left( x \right);m = \mathop {\min }\limits_{\left[ { – 2;2} \right]} f\left( x \right)\) bằng bao nhiêu.
b) Giải phương trình \(f’\left( x \right) = 0\) với \(x \in \left( { – 2;2} \right)\)
c) Tính các giá trị của hàm số \(f\left( x \right)\) tại hai đầu mút \( – 2;2\) và tại các điểm \(x \in \left( { – 2;2} \right)\) mà ở đó \(f’\left( x \right) = 0\)
d) So sánh M (hoặc m) với số lớn nhất (hoặc số bé nhất) trong các giá trị tính được ở câu c
Lời giải:
a) Ta có: \(\left\{ \begin{array}{l}\mathop {\max }\limits_{\left[ { – 2;2} \right]} f\left( x \right) = 4\\\mathop {\min }\limits_{\left[ { – 2;2} \right]} f\left( x \right) = – 4\end{array} \right.\).
b) Ta có: \(f’\left( x \right) = 6{x^2} – 6\).
Xét \(f’\left( x \right) = 0 \Leftrightarrow x = \pm 1\).
c) Ta có:\(\left\{ \begin{array}{l}f\left( 2 \right) = f\left( { – 1} \right) = 4\\f\left( { – 2} \right) = f\left( 1 \right) = – 4\end{array} \right.\).
d) Nhận xét: \(\left\{ \begin{array}{l}\mathop {\max }\limits_{\left[ { – 2;2} \right]} f\left( x \right) = f\left( 2 \right) = f\left( { – 1} \right)\\\mathop {\min }\limits_{\left[ { – 2;2} \right]} f\left( x \right) = f\left( { – 2} \right) = f\left( 1 \right)\end{array} \right.\).