Hướng dẫn giải Câu hỏi Hoạt động 2 trang 30 SGK Toán 12 Cánh diều – Bài 4. Ứng dụng hình học của tích phân. Gợi ý: Quan sát hình vẽ.
Câu hỏi/Đề bài:
Cho các hàm số \(y = {2^x}\), y = x
Gọi \({S_1}\) là diện tích hình phẳng giới hạn bởi trục Ox, hai đường thẳng x = 1, x = 2 và đồ thị hàm số \(y = {2^x}\)
Gọi \({S_2}\) là diện tích hình phẳng giới hạn bởi trục Ox, hai đường thẳng x = 1, x = 2 và đồ thị hàm số y = x
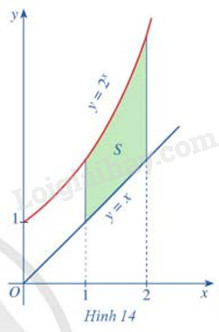
Gọi S là phẳng giới hạn bởi các đồ thị hàm số \(y = {2^x}\), y = x và hai đường thẳng x = 1, x = 2
(Hình 14)
a) Biểu diễn S theo \({S_1},{S_2}\)
b) So sánh S và \(\int\limits_1^2 {({2^x} – x)dx} \)
Hướng dẫn:
Quan sát hình vẽ
Lời giải:
a) \(S = {S_1} – {S_2}\)
b) \(S = {S_1} – {S_2}\)
\(\int\limits_1^2 {({2^x} – x)dx} = \int\limits_1^2 {{2^x}dx} – \int\limits_1^2 {xdx} = {S_1} – {S_2}\)
Vậy S = \(\int\limits_1^2 {({2^x} – x)dx} \)