B1: Tìm tập xác định của hàm số. B2: Tính đạo hàm. Hướng dẫn giải Giải bài tập 6 trang 14 SGK Toán 12 tập 1 – Cánh diều – Bài 1. Tính đơn điệu của hàm số. Thể tích V (đơn vị: centimet khối) của 1kg nước tại nhiệt độ T\(\left( {0{{\rm{ }}^o}C \le T \le 30{{\rm{…
Đề bài/câu hỏi:
Thể tích V (đơn vị: centimet khối) của 1kg nước tại nhiệt độ T\(\left( {0{{\rm{ }}^o}C \le T \le 30{{\rm{ }}^o}C} \right)\) được tính bởi công thức sau:
\(V\left( T \right) = 999,87 – 0,06426T + 0,0085043{T^2} – 0,0000679{T^3}\).
Hỏi thể tích \(V\left( T \right)\),\(\left( {0{{\rm{ }}^o}C \le T \le 30{{\rm{ }}^o}C} \right)\) giảm trong khoảng nhiệt độ nào?
Hướng dẫn:
B1: Tìm tập xác định của hàm số.
B2: Tính đạo hàm. Tìm các điểm mà tại đó đạo hàm bằng không hoặc không tồn tại.
B3: Lập bảng biến thiên.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải:
Tập xác định: \(D = \mathbb{R}\).
Ta có: \(V’\left( T \right) = – 0,06426 + 2 \times 0,0085043 \times T – 3 \times 0,0000679{T^2}\).
Nhận xét \(V’\left( T \right) = 0 \Leftrightarrow \left[ \begin{array}{l}T \approx 79,5\\T \approx 3,97\end{array} \right.\).
Ta có bảng biến thiên sau:
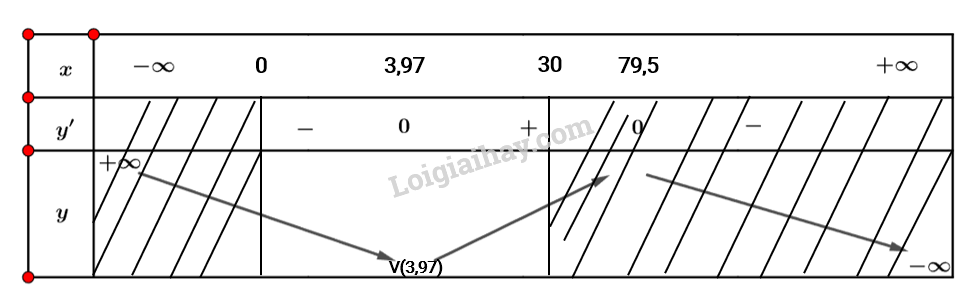
Vậy thể tích giảm trong khoảng nhiệt độ từ \(\left( {{0^o};3,{{97}^o}} \right)\).