\({s^2} = \frac{{{n_1}. {{({x_1} – \overline x )}^2} + {n_2}{{({x_2} – \overline x )}^2} + . . . + {n_p}{{({x_p} – \overline x )}^2}}}{n}\. Trả lời Giải bài tập 3 trang 92 SGK Toán 12 tập 1 – Cánh diều – Bài 2. Phương sai – độ lệch chuẩn của mẫu số liệu ghép nhóm. Bảng 21 biểu diễn mẫu số liệu ghép nhóm về độ tuổi của cư dân trong một khu phố….
Đề bài/câu hỏi:
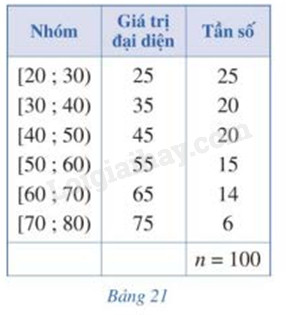
Bảng 21 biểu diễn mẫu số liệu ghép nhóm về độ tuổi của cư dân trong một khu phố. Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.
Hướng dẫn:
\({s^2} = \frac{{{n_1}.{{({x_1} – \overline x )}^2} + {n_2}{{({x_2} – \overline x )}^2} + … + {n_p}{{({x_p} – \overline x )}^2}}}{n}\)
\(s = \sqrt {{s^2}} \)
Lời giải:
Số trung bình cộng của mẫu số liệu ghép nhóm là: \(\overline x = \frac{{25.25 + 20.35 + 20.45 + 15.55 + 14.65 + 6.75}}{{100}} = 44,1\)
Phương sai của mẫu số liệu ghép nhóm là:
\({s^2} = \frac{{25.{{(25 – 44,1)}^2} + 20.{{(35 – 44,1)}^2} + 20.{{(45 – 44,1)}^2} + 15.{{(55 – 44,1)}^2} + 14.{{(65 – 44,1)}^2} + 6.{{(75 – 44,1)}^2}}}{{100}} = 244,19\)
Độ lệch chuẩn của mẫu số liệu ghép nhóm là: \(s = \sqrt {{s^2}} = \sqrt {244,19} \approx 15,63\)