B1: Tìm tập xác định của hàm số. B2: Tính \(y’\). Tìm các điểm mà tại đó \(y’ = 0\) hoặc \(y’\) không tồn tại. Hướng dẫn cách giải/trả lời Giải bài tập 3 trang 13 SGK Toán 12 tập 1 – Cánh diều – Bài 1. Tính đơn điệu của hàm số. Tìm các khoảng đơn điệu của hàm số sau: a) \(y = – {x^3} + 2{x^2} – 3\…
Đề bài/câu hỏi:
Tìm các khoảng đơn điệu của hàm số sau:a) \(y = – {x^3} + 2{x^2} – 3\) b) \(y = {x^4} – 2{x^2} + 5\)c) \(y = \frac{{3x + 1}}{{2 – x}}\) d) \(y = \frac{{{x^2} – 2x}}{{x + 1}}\)
Hướng dẫn:
B1: Tìm tập xác định của hàm số.
B2: Tính \(y’\). Tìm các điểm mà tại đó \(y’ = 0\) hoặc \(y’\) không tồn tại.
B3: Lập bảng biến thiên của hàm số.
B4: Dựa vào bảng biến thiên để kết luận.
Lời giải:
a) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y’ = – 3{x^2} + 4x\).
Nhận xét \(y’ = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \frac{4}{3}\end{array} \right.\)
Ta có bảng biến thiên sau:
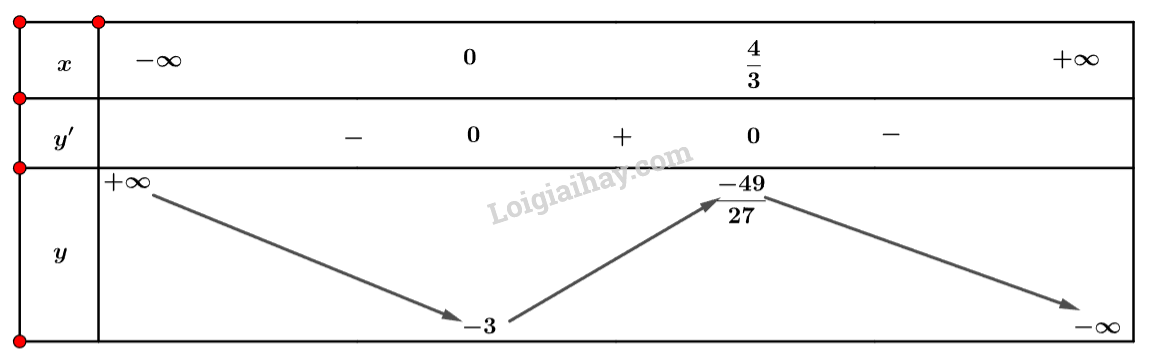
Vậy hàm số đồng biến trên khoảng \(\left( {0;\frac{4}{3}} \right)\) và nghịch biến trên khoảng \(\left( { – \infty ;0} \right)\) và \(\left( {\frac{4}{3}; + \infty } \right)\).
b) Tập xác định: \(D = \mathbb{R}\).
Ta có: \(y’ = 4{x^3} – 4x\).
Nhận xét \(y’ = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm 1\end{array} \right.\)
Ta có bảng biến thiên sau:
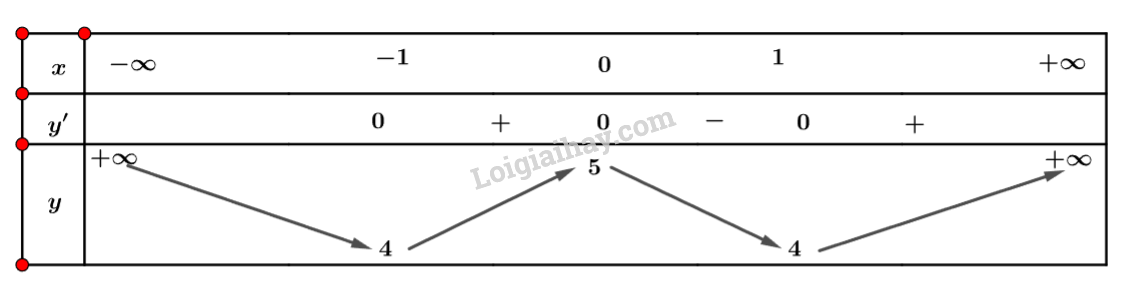
Vậy hàm số đồng biến trên khoảng \(\left( { – 1;0} \right)\) và \(\left( {1; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { – \infty ; – 1} \right)\) và \(\left( {0;1} \right)\).
c) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 2 \right\}\).
Ta có: \(y’ = \frac{5}{{{{\left( {2 – x} \right)}^2}}}\).
Nhận xét \(y’ > 0{\rm{ }}\forall x \in D\)
Ta có bảng biến thiên sau:
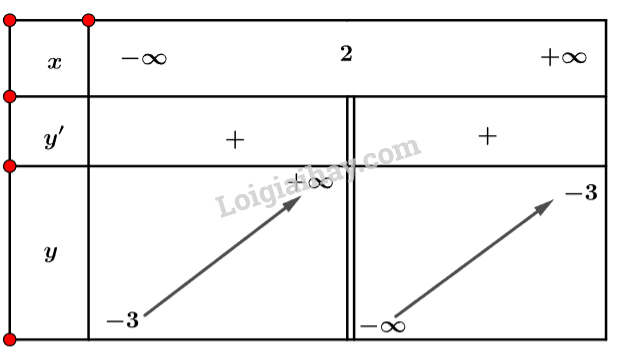
Vậy hàm số đồng biến trên khoảng \(\left( { – \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\).
d) Tập xác định: \(D = \mathbb{R}\backslash \left\{ { – 1} \right\}\).
Ta có: \(y’ = \frac{{\left( {2x – 2} \right)\left( {x + 1} \right) – {x^2} + 2x}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{{x^2} + 2x – 2}}{{{{\left( {x + 1} \right)}^2}}}\).
Nhận xét \(y’ = 0 \Leftrightarrow \left[ \begin{array}{l}x = – 1 + \sqrt 3 \\x = – 1 – \sqrt 3 \end{array} \right.\).
Ta có bảng biến thiên sau:
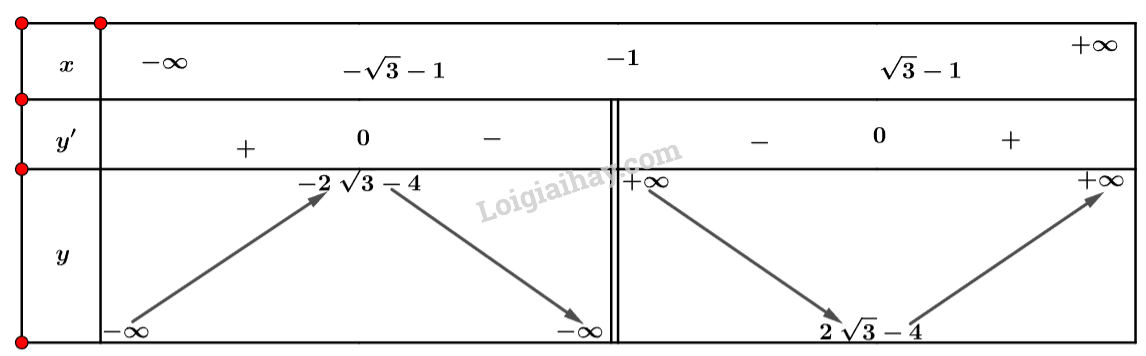
Vậy hàm số đồng biến trên khoảng \(\left( { – \infty ; – 1 – \sqrt 3 } \right)\) và \(\left( { – 1 + \sqrt 3 ; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { – 1 – \sqrt 3 ; – 1} \right)\) và \(\left( { – 1; – 1 + \sqrt 3 } \right)\).