Vì đèn cân bằng nên trọng lực của đèn sẽ phân bố đều trên các chân của giá đỡ. Trả lời Giải bài tập 15 trang 83 SGK Toán 12 tập 1 – Cánh diều – Bài tập cuối chương 2. Một chiếc máy được đặt trên một giá đỡ ba chân với điểm đặt E(0;0;…
Đề bài/câu hỏi:
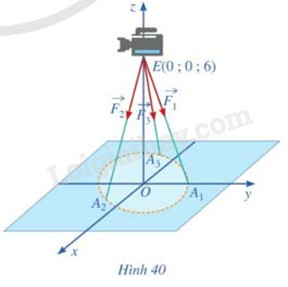
Một chiếc máy được đặt trên một giá đỡ ba chân với điểm đặt E(0;0;6) và các điểm tiếp xúc với mặt đất của ba chân lần lượt là \({A_1}(0;1;0)\), \({A_2}(\frac{{\sqrt 3 }}{2}; – \frac{1}{2};0)\), \({A_3}( – \frac{{\sqrt 3 }}{2}; – \frac{1}{2};0)\) (Hình 40). Biết rằng trọng lượng của chiếc máy là 300N. Tìm tọa độ của các lực tác dụng lên giá đỡ \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \)
Hướng dẫn:
Vì đèn cân bằng nên trọng lực của đèn sẽ phân bố đều trên các chân của giá đỡ. Từ tọa độ các điểm đã cho, ta tìm được cái mối liên hệ với vecto lực và tìm được tọa độ của các vecto lực
Lời giải:
Ta có: \(\overrightarrow {E{A_1}} = (0;1; – 6);\overrightarrow {E{A_2}} = (\frac{{\sqrt 3 }}{2}; – \frac{1}{2}; – 6);\overrightarrow {E{A_3}} = ( – \frac{{\sqrt 3 }}{2}; – \frac{1}{2}; – 6) \Rightarrow E{A_1} = E{A_2} = E{A_3} = \sqrt {37} \)
\(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_3}} } \right|\) vì đèn cân bằng và trọng lực của đèn tác dụng đều lên 3 chân của giá đỡ
Do đó:
\(\overrightarrow {{F_1}} = k\overrightarrow {E{A_1}} = (0;k; – 6k)\)
\(\overrightarrow {{F_2}} = k\overrightarrow {E{A_2}} = (\frac{{\sqrt 3 }}{2}k; – \frac{1}{2}k; – 6k)\)
\(\overrightarrow {{F_3}} = k\overrightarrow {E{A_3}} = ( – \frac{{\sqrt 3 }}{2}k; – \frac{1}{2}k; – 6k)\)
\( \Rightarrow \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = (0;0; – 18k)\)
Mà \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow P = (0;0; – 300) \Rightarrow – 18k = 300 \Leftrightarrow k = \frac{{50}}{3}\)
Vậy \(\overrightarrow {{F_1}} = (0;\frac{{50}}{3}; – 100)\); \(\overrightarrow {{F_2}} = (\frac{{25\sqrt 3 }}{3}; – \frac{{50}}{6}; – 100)\);\(\overrightarrow {{F_3}} = ( – \frac{{25\sqrt 3 }}{3}; – \frac{{50}}{6}; – 100)\)