Ý a: Sử dụng một số kiến thức về hình học phẳng và hình lăng trụ để tìm được diện tích đáy và chiều cao. Trả lời Giải bài 1.68 trang 37 sách bài tập toán 12 – Kết nối tri thức – Bài tập cuối chương 1. Một hành lang giữa hai nhà có hình dạng của một lăng trụ đứng (xem hình bên)….
Đề bài/câu hỏi:
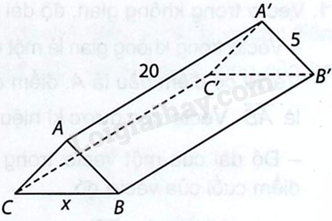
Một hành lang giữa hai nhà có hình dạng của một lăng trụ đứng (xem hình bên). Hai mặt bên ABB’A’ và ACC’A’ là hai tấm kính hình chữ nhật dài 20 m, rộng 5 m. Gọi x (m) là độ dài của cạnh BC.
a) Tính thể tích V của hình lăng trụ theo x.
b) Tìm x sao cho hình lăng trụ có thể tích lớn nhất và tính giá trị lớn nhất đó.
Hướng dẫn:
Ý a: Sử dụng một số kiến thức về hình học phẳng và hình lăng trụ để tìm được diện tích đáy và chiều cao, từ đó tính được thể tích V.
Ý b: Xét hàm số V theo x trên \(\left( {0;10} \right)\) sau đó lập bảng biến thiên và tìm giá trị lớn nhất của hàm số.
Lời giải:
a) Ta thấy do ABB’A’ và ACC’A’ là hai tấm kính hình chữ nhật có kích thước giống nhau nên \(AC = AB\) (đều là chiều rộng của mặt hình chữ nhật) do đó đáy \(ABC\)là tam giác cân tại
\(A\). Gọi \(H\) là trung điểm cạnh \(AB\) suy ra \(AH\) là đường cao của tam giác (tính chất tam giác cân). Ta có \(AH = \sqrt {A{B^2} – B{H^2}} = \sqrt {25 – {{\left( {\frac{x}{2}} \right)}^2}} = \frac{1}{2}\sqrt {100 – {x^2}} \).
Diện tích tam giác ABC là \(S = \frac{1}{2}BC \cdot AH = \frac{1}{2}x \cdot \frac{1}{2}\sqrt {100 – {x^2}} = \frac{1}{4}x\sqrt {100 – {x^2}} \).
Thể tích khối lăng trụ là \(V = S \cdot AA’ = 5x\sqrt {100 – {x^2}} \) (m3) với \(0 < x < 10\).
b) Xét hàm số \(V = 5x\sqrt {100 – {x^2}} \) trên \(\left( {0;10} \right)\).
Ta có \(V’ = 5x\sqrt {100 – {x^2}} + 5x\frac{{ – 2x}}{{2\sqrt {100 – {x^2}} }} = \frac{{500 – 10{x^2}}}{{\sqrt {100 – {x^2}} }};\)
Suy ra \(V’ = 0 \Leftrightarrow 500 – 10{x^2} = 0 \Leftrightarrow x = 5\sqrt 2 \) do \(x > 0\).
Lập bảng biến thiên:
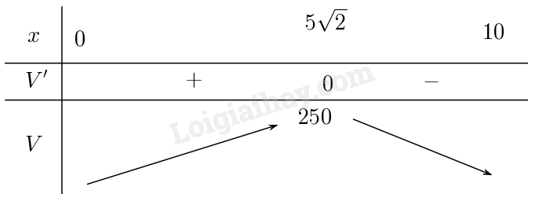
Vậy hình lăng trụ có thể tích lớn nhất khi \(x = 5\sqrt 2 \) (m). \(\mathop {\max }\limits_{\left( {0;10} \right)} V = V\left( {5\sqrt 2 } \right) = 250\) (m3).