Quan sát đồ thị và tính đạo hàm, nhận xét về sự biến thiên, tiệm cận. Phân tích và giải Giải bài 1.61 trang 35 sách bài tập toán 12 – Kết nối tri thức – Bài tập cuối chương 1. Cho hàm số (y = frac{{ax + b}}{{cx + d}}) có đồ thị như hình vẽ sau:…
Đề bài/câu hỏi:
Cho hàm số \(y = \frac{{ax + b}}{{cx + d}}\) có đồ thị như hình vẽ sau:
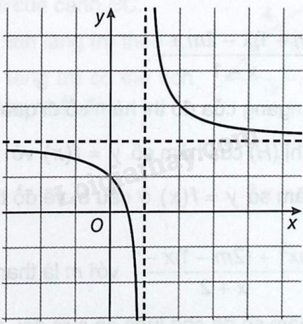
Mệnh đề nào sau đây là mệnh đề đúng?
A. \(bc < ad < 0\)
B. \(ad < 0 < bc\)
C. \(0 < ad < bc\)
D. \(ad < bc < 0\)
Hướng dẫn:
Quan sát đồ thị và tính đạo hàm, nhận xét về sự biến thiên, tiệm cận, giao điểm với hai trục tọa độ của đồ thị hàm số.
Lời giải:
Đáp án: D.
Ta có \(y’ = \frac{{ad – bc}}{{cx + d}}\). Từ đồ thị ta thấy hàm số nghịch biến trên tập xác định của nó.
Suy ra \(y’ < 0 \Leftrightarrow \frac{{ad – bc}}{{cx + d}} < 0 \Leftrightarrow ad – bc < 0 \Leftrightarrow ad < bc\). Từ đó ta loại đáp án A.
Quan sát ba đáp án còn lại, ta cần tìm dấu của \(ad\) và \(bc\) để chọn được đáp án đúng (so sánh với 0).
Xét giao điểm của đồ thị với các trục:
+ Trục hoành: giao điểm là \(\left( {\frac{{ – b}}{a};0} \right)\) có hoành độ dương suy ra \(\frac{{ – b}}{a} > 0 \Leftrightarrow ab < 0\). Do đó \(a\) và \(b\) trái dấu.
+ Trục tung: giao điểm là \(\left( {0;\frac{b}{d}} \right)\) có tung độ dương suy ra \(\frac{b}{d} > 0 \Leftrightarrow bd > 0\). Do đó \(b\) và \(d\) cùng dấu.
Suy ra \(a\) và \(d\) trái dấu hay \(ad < 0\). Do đó ta loại tiếp đáp án C.
Ta có \(\mathop {\lim }\limits_{x \to + \infty } y = \frac{{ax + b}}{{cx + d}} = \frac{a}{c}\) suy ra đồ thị có tiệm cận ngang là đường thẳng \(y = \frac{a}{c}\).
Mà tiệm cận ngang là đường thẳng nằm phía trên trục hoành (quan sát hình vẽ), nên \(\frac{a}{c} > 0 \Leftrightarrow ac > 0\).
Hay \(a\) và \(c\) cùng dấu. Vì \(a\) và \(b\) trái dấu (đã chứng minh) nên \(c\)và \(b\) trái dấu hay \(bc < 0\), ta loại đáp án B.
Vậy ta chọn đáp án D.