Ý a: Xét sự biến thiên của hàm số \(H\left( v \right) = 33\left( {10\sqrt v – v + 10, 45} \right)\). Hướng dẫn cách giải/trả lời Giải bài 1.46 trang 32 sách bài tập toán 12 – Kết nối tri thức – Bài 5. Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn. Ở ({0^ circ }C), sự mất nhiệt (H) (tính bằng Kcal/m2h,…
Đề bài/câu hỏi:
Ở \({0^ \circ }C\), sự mất nhiệt \(H\) (tính bằng Kcal/m2h, ở đây Kcal là kilocalories và 1 Kcal=1000 calo) từ cơ thể của một người có thể được mô hình hóa bằng công thức
\(H = 33\left( {10\sqrt v – v + 10,45} \right),\)
Trong đó \(v\) là tốc độ gió (tính bằng m/s) (Theo sách Brief Calculus: An Applied Approach, 8th edition, Cengage Learning, 2009).
a) Xét tính đơn điệu của hàm số \(H\) và giải thích ý nghĩa thực tiễn của kết quả nhận được.
b) Tìm tốc độ thay đổi của \(H\) khi \(v = 2\) m/s. Giải thích ý nghĩa thực tiễn của kết quả này.
Hướng dẫn:
Ý a: Xét sự biến thiên của hàm số \(H\left( v \right) = 33\left( {10\sqrt v – v + 10,45} \right)\), sau đó nhận xét về mối liên hệ giữa mức nhiệt mất từ cơ thể và tốc độ gió.
Ý b: Tính \(H’\left( 2 \right)\), giá trị này là mức nhiệt của cơ thể mất tiếp khi vận tốc gió tăng từ \(2\) m/s lên \(3\) m/s.
Lời giải:
a) Xét hàm số \(H\left( v \right) = 33\left( {10\sqrt v – v + 10,45} \right)\).
Ta có \(H’\left( v \right) = 33\left( {\frac{5}{{\sqrt v }} – 1} \right),{\rm{ v > }}0\). Khi đó \(H’\left( v \right) = 0 \Leftrightarrow 33\left( {\frac{5}{{\sqrt v }} – 1} \right) = 0 \Leftrightarrow v = 25\).
Lập bảng biến thiên:
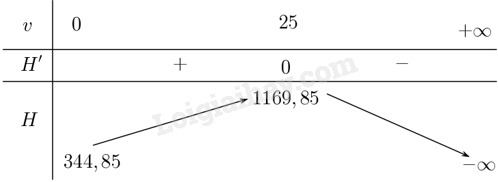
Từ bảng biến thiên suy ra \(H\) đồng biến trên khoảng \(\left( {25; + \infty } \right)\), nghịch biến trên khoảng \(\left( {0;25} \right)\)
Do đó, mức nhiệt mất từ cơ thể tăng khi tốc độ gió tăng không vượt quá 25 m/s, đạt tối đa ở mức gió 25 m/s và sau đó giảm dần khi tốc độ gió tiếp tục tăng.
b) Ta có \(H’\left( 2 \right) = 33\left( {\frac{5}{{\sqrt 2 }} – 1} \right) \approx 83,673\).
Điều này có nghĩa là mức nhiệt của cơ thể mất tiếp khi vận tốc gió tăng từ \(2\) m/s lên \(3\) m/s là khoảng \(83,673\) (Kcal/m2h).