Bài 1.37 trang 26 SBT toán 12 – Kết nối tri thức: Giả sử chi phí để sản xuất x sản phẩm của một nhà máy được cho bởi C x = 0, 2x^2 + 10x + 5 (triệu đồng)

Đề bài/câu hỏi:

Giả sử chi phí để sản xuất \(x\) sản phẩm của một nhà máy được cho bởi \(C\left( x \right) = 0,2{x^2} + 10x + 5\) (triệu đồng). Khi đó chi phí trung bình để sản xuất một đơn vị sản phẩm là \(f\left( x \right) = \frac{{C\left( x \right)}}{x}\).

a) Khảo sát sự biến thiên của hàm số \(y = f\left( x \right)\).

b) Số lượng sản phẩm cần sản xuất là bao nhiêu để chi phí trung bình là thấp nhất?

Hướng dẫn:

Ý a: Khảo sát hàm số \(y = f\left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{0,2{x^2} + 10x + 5}}{x}\) theo các bước đã học.

Ý b: Từ bảng biến thiên suy ra giá trị nhỏ nhất của hàm số.

Lời giải:

a) Xét hàm số \(y = f\left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{0,2{x^2} + 10x + 5}}{x}\) .

Tập xác định \(\left[ {1; + \infty } \right)\).

Sự biến thiên: \(f’\left( x \right) = {\left( {\frac{{0,2{x^2} + 10x + 5}}{x}} \right)^\prime } = \frac{{0,2{x^2} – 5}}{{{x^2}}}\).

Khi đó \(f’\left( x \right) = 0 \Leftrightarrow \frac{{0,2{x^2} – 5}}{{{x^2}}} = 0 \Leftrightarrow x = 5\) do \(x \ge 1\).

+ Ta có \(S’\left( x \right) = 0 \Leftrightarrow \frac{{6{{\left( {x – 4} \right)}^2} – 1200}}{{{{\left( {x – 4} \right)}^2}}} = 0 \Leftrightarrow 6{\left( {x – 4} \right)^2} – 1200 = 0 \Leftrightarrow x = 4 + 10\sqrt 2 \).

+ Hàm số đồng biến trên khoảng \(\left( {5; + \infty } \right)\), nghịch biến trên khoảng \(\left( {1;5} \right)\).

+ Hàm số đạt cực tiểu tại \(x = 5\) với \({f_{CT}} = 12\).

+ Giới hạn tại vô cực \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \)

+ Bảng biến thiên:

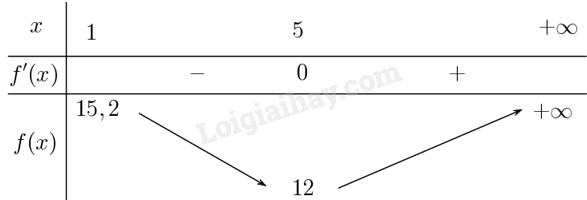
b) Từ bảng biến thiên suy ra số lượng sản phẩm cần sản xuất là \(x = 5\) để chi phí sản xuất trung bình là thấp nhất: \({f_{CT}} = 12\).