Xét hàm số \(h\left( t \right)\) trên đoạn \(\left[ {0;20} \right]\), lập bảng biến thiên và tìm khoảng đồng biến, nghịch biến của hàm số. Phân tích và giải Giải bài 11 trang 11 sách bài tập toán 12 – Chân trời sáng tạo – Bài 1. Tính đơn điệu và cực trị của hàm số. Độ cao (tính bằng mét) của tàu lượn siêu tốc so với mặt đất sau \(t\…
Đề bài/câu hỏi:
Độ cao (tính bằng mét) của tàu lượn siêu tốc so với mặt đất sau \(t\)(giây) \(\left( {0 \le t \le 20} \right)\) từ lúc bắt đầu được cho bởi công thức
\(h\left( t \right) = – \frac{4}{{255}}{t^3} + \frac{{49}}{{85}}{t^2} – \frac{{98}}{{17}}t + 20\).
Trong khoảng thời gian nào tàu lượn đi xuống, trong khoảng thời gian nào tàu lượn đi lên?
Hướng dẫn:
Xét hàm số \(h\left( t \right)\) trên đoạn \(\left[ {0;20} \right]\), lập bảng biến thiên và tìm khoảng đồng biến, nghịch biến của hàm số.
Lời giải:
Xét hàm số \(h\left( t \right) = – \frac{4}{{255}}{t^3} + \frac{{49}}{{85}}{t^2} – \frac{{98}}{{17}}t + 20\) trên đoạn \(\left[ {0;20} \right]\).
Ta có: \(h’\left( t \right) = – \frac{4}{{85}}{t^2} + \frac{{98}}{{85}}t – \frac{{98}}{{17}};h’\left( t \right) = 0 \Leftrightarrow t = \frac{{35}}{2}\) hoặc \(t = 7\).
Bảng biến thiên:
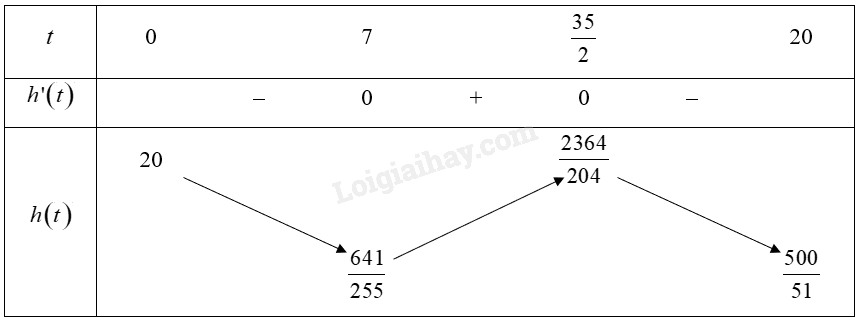
Vậy hàm số đồng biến trên khoảng \(\left( {7;\frac{{35}}{2}} \right)\), hàm số nghịch biến trên các khoảng \(\left( {0;7} \right)\) và \(\left( {\frac{{35}}{2};20} \right)\).
Vậy tàu lượn đi lên trong khoảng thời gian từ 7 giây đến 17,5 giây, tàu lượn đi xuống trong khoảng thời gian từ 0 giây đến 7 giây và từ 17,5 giây đến 20 giây.