‒ Sử dụng công thức tính khoảng biến thiên của mẫu số liệu ghép nhóm: \(R = {a_{m + 1}} – {a_1}\). Gợi ý giải Giải bài 7 trang 92 sách bài tập toán 12 – Cánh diều – Bài 1. Khoảng biến thiên – khoảng tứ phân vị của mẫu số liệu ghép nhóm. Một cuộc khảo sát xác định số năm đã sử dụng của 160 chiếc ô tô….
Đề bài/câu hỏi:
Một cuộc khảo sát xác định số năm đã sử dụng của 160 chiếc ô tô. Kết quả điều tra được cho trong Bảng 10.
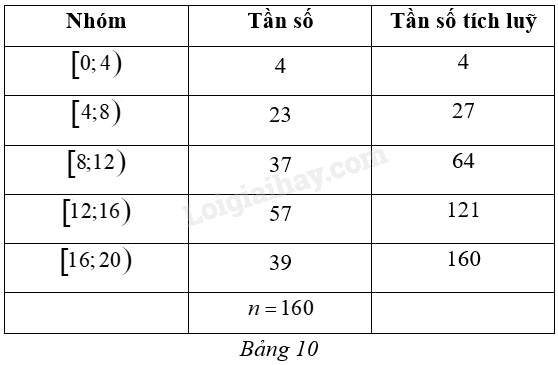
a) Tính khoảng biến thiên của mẫu số liệu ghép nhóm đó.
b) Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đó (làm tròn kết quả đến hàng phần mười).
Hướng dẫn:
‒ Sử dụng công thức tính khoảng biến thiên của mẫu số liệu ghép nhóm: \(R = {a_{m + 1}} – {a_1}\).
‒ Sử dụng công thức tính các tứ phân vị của mẫu số liệu ghép nhóm:
+ Nhóm thứ \(p\) là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{n}{4}\) (tức là \(c{f_{p – 1}} < \frac{n}{4}\) nhưng \(c{f_p} \ge \frac{n}{4}\)). Ta gọi \(s,h,{n_p}\) lần lượt là đầu mút trái, độ dài, tần số của nhóm \(p\), \(c{f_{p – 1}}\) là tần số tích luỹ của nhóm thứ \(p – 1\). Khi đó: \({Q_1} = s + \left( {\frac{{\frac{n}{4} – c{f_{p – 1}}}}{{{n_p}}}} \right).h\).
+ Nhóm thứ \(q\) là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{{3n}}{4}\) (tức là \(c{f_{q – 1}} < \frac{{3n}}{4}\) nhưng \(c{f_q} \ge \frac{{3n}}{4}\)). Ta gọi \(t,l,{n_q}\) lần lượt là đầu mút trái, độ dài, tần số của nhóm \(q\), \(c{f_{q – 1}}\) là tần số tích luỹ của nhóm thứ \(q – 1\). Khi đó: \({Q_3} = t + \left( {\frac{{\frac{{3n}}{4} – c{f_{q – 1}}}}{{{n_q}}}} \right).l\).
‒ Sử dụng công thức tính khoảng tứ phân vị của mẫu số liệu ghép nhóm: \(\Delta Q = {Q_3} – {Q_1}\).
Lời giải:
a) Khoảng biến thiên của mẫu số liệu ghép nhóm đó là: \(R = 20 – 0 = 20\) (năm).
b) Nhóm 3 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{n}{4} = \frac{{160}}{4} = 40\).
Nhóm 3 có đầu mút trái \(s = 8\), độ dài \(h = 4\), tần số của nhóm \({n_3} = 37\) và nhóm 2 có tần số tích luỹ \(c{f_2} = 27\).
Ta có: \({Q_1} = s + \left( {\frac{{40 – c{f_2}}}{{{n_3}}}} \right).h = 8 + \left( {\frac{{40 – 27}}{{37}}} \right).4 = \frac{{348}}{{37}}\) (năm).
Nhóm 4 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng \(\frac{{3n}}{4} = \frac{{3.160}}{4} = 120\).
Nhóm 4 có đầu mút trái \(t = 12\), độ dài \(l = 4\), tần số của nhóm \({n_4} = 57\) và nhóm 3 có tần số tích luỹ \(c{f_3} = 64\).
Ta có: \({Q_3} = t + \left( {\frac{{120 – c{f_3}}}{{{n_4}}}} \right).l = 12 + \left( {\frac{{120 – 64}}{{57}}} \right).4 = \frac{{908}}{{57}}\) (năm).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \(\Delta Q = {Q_3} – {Q_1} = \frac{{908}}{{57}} – \frac{{348}}{{37}} \approx 6,5\) (năm).