Dựa vào đồ thị hàm số xác định các khoảng đơn điệu của hàm số. Hướng dẫn giải Giải bài 7 trang 11 sách bài tập toán 12 – Cánh diều – Bài 1. Tính đơn điệu của hàm số. Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như Hình 4….
Đề bài/câu hỏi:
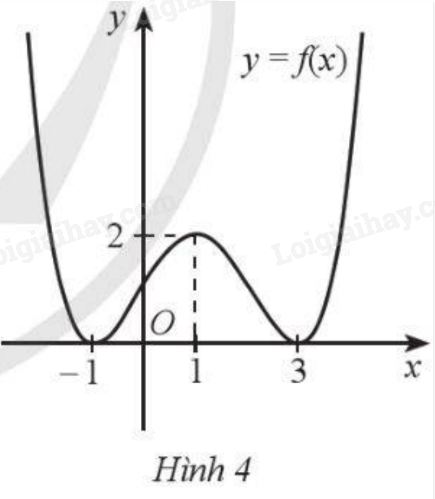
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như Hình 4. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A. \(\left( { – \infty ;0} \right)\).
B. \(\left( {3; + \infty } \right)\).
C. \(\left( { – 1;1} \right)\).
D. \(\left( { – \infty ; – 1} \right)\).
Hướng dẫn:
Dựa vào đồ thị hàm số xác định các khoảng đơn điệu của hàm số:
+ Khoảng đồng biến có đồ thị “đi lên” từ trái sang phải.
+ Khoảng nghịch biến có đồ thị “đi xuống” từ trái sang phải.
Lời giải:
Dựa vào đồ thị ta có:
Hàm số đồng biến trên các khoảng \(\left( { – 1;1} \right)\) và \(\left( {3; + \infty } \right)\).
Hàm số nghịch biến trên các khoảng \(\left( { – \infty ; – 1} \right)\) và \(\left( {1;3} \right)\).
Chọn D.