‒ Tìm công thức xác định hàm số mô phỏng thể tích \(V\) của hình hộp chữ nhật. Trả lời Giải bài 109 trang 44 sách bài tập toán 12 – Cánh diều – Bài tập cuối chương 1. Từ một miếng bìa có độ dài hai cạnh lần lượt là 0,9 m và 1,5 m như Hình 32….
Đề bài/câu hỏi:
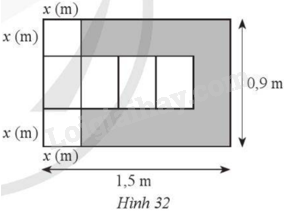
Từ một miếng bìa có độ dài hai cạnh lần lượt là 0,9 m và 1,5 m như Hình 32. Bạn Minh cắt đi phần tô màu xám và gấp lại để được một hình hộp chữ nhật. Gọi \(V\) là thể tích hình hộp chữ nhật được tạo thành, \(V\) được tính theo \(x\) bởi công thức nào? Tìm \(x\) để hình hộp tạo thành có thể tích lớn nhất.
Hướng dẫn:
‒ Tìm công thức xác định hàm số mô phỏng thể tích \(V\) của hình hộp chữ nhật.
‒ Dựa vào công thức của hàm số để tìm giá trị lớn nhất của hàm số.
Lời giải:
Do chiều dài của miếng bìa sau khi cắt đi thì độ dài dài nhất còn lại là \(4{\rm{x}}\) nên ta có:
\(0 < 4{\rm{x}} < 1,5 \Leftrightarrow 0 < {\rm{x}} < 0,375\)
Theo đề bài ta có:
Chiều dài đáy của hình hộp chữ nhật là: .
Chiều rộng đáy của hình hộp chữ nhật là: \({\rm{x}}\left( m \right)\).
Chiều cao của hình hộp chữ nhật là: \({\rm{x}}\left( m \right)\).
Khi đó, thể tích của hình hộp chữ nhật là: \(V = {x^2}\left( {0,9 – 2{\rm{x}}} \right)\left( {{m^3}} \right)\).
Xét hàm số \(V\left( x \right) = {x^2}\left( {0,9 – 2{\rm{x}}} \right) = – 2{{\rm{x}}^3} + 0,9{{\rm{x}}^2}\) trên \(\left( {0;0,375} \right)\).
Ta có: \(V’\left( x \right) = – 6{x^2} + 1,8{\rm{x}}\)
Khi đó, trên khoảng \(\left( {0;0,375} \right)\), \(V’\left( x \right) = 0\) khi \(x = 0,3\).
Bảng biến thiên:
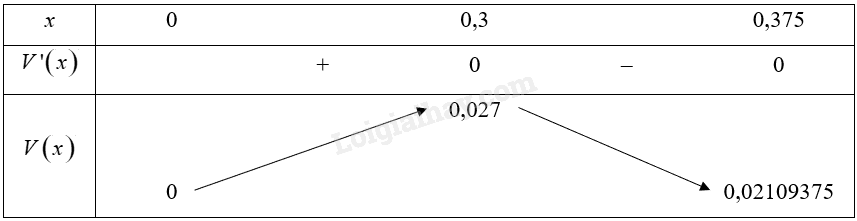
Vậy \(\mathop {\max }\limits_{\left( {0;0,375} \right)} V\left( x \right) = 0,027\) tại \(x = 0,3\).
Vậy khi \(x = 0,3\left( m \right)\) thì hình hộp tạo thành có thể tích lớn nhất.