Giải chi tiết Câu 1 trang 10 Bài 2. Mô tả dao động điều hòa SGK Vật Lí 11 Kết nối tri thức. Tham khảo: Quan sát hình vẽ và dựa vào kiến thức đã học.
Câu hỏi/Đề bài:
Hình 2.1 là đồ thị dao động điều hoà của một vật.
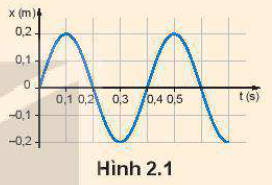
Hãy xác định:
– Biên độ, chu kì, tần số của dao động.
– Nêu thời điểm mà vật có li độ \(x = 0;x = 0,1\;m\).
Hướng dẫn:
Quan sát hình vẽ và dựa vào kiến thức đã học
– Biên độ: \(A\) là độ dịch chuyển cực đại của vật tính từ vị trí cân bằng.
– Chu kì: là khoảng thời gian để vật thực hiện được một dao động, kí hiệu là \(T\).
– Tần số: là số dao động mà vật thực hiện được trong một giây, kí hiệu là \(f\).
Ta có: \(f = \frac{1}{{\;T}}\)
– Viết phương trình dao động điều hoà và thay li độ vào phương trình để tính thời điểm.
Lời giải:
– Từ đồ thị ta thấy:
Biên độ: \(A = 0,2\left( m \right) = 20\left( {cm} \right)\)
Chu kì: \(T = 0,4\left( s \right)\)
Tần số: \(f = \frac{1}{T} = \frac{1}{{0,4}} = 2,5\left( {Hz} \right)\)
– Tần số góc của dao động điều hoà: \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,4}} = 5\pi \) (rad/s)
Từ đồ thị ta thấy lúc \(t = 0\) thì \(x = 0\) và đang đi về biên dương
\( \Rightarrow \left\{ \begin{array}{l}0 = A.\cos \varphi \\ – \omega A\sin \varphi > 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\cos \varphi = 0\\\sin \varphi < 0\end{array} \right. \Rightarrow \varphi = – \frac{\pi }{2}\)
Phương trình dao động điều hoà: \(x = 20\cos \left( {5\pi t – \frac{\pi }{2}} \right)\) cm.
+ Thời điểm vật có li độ \(x = 0\) là:
\(\begin{array}{l}20\cos \left( {5\pi t – \frac{\pi }{2}} \right) = 0 \Leftrightarrow \cos \left( {5\pi t – \frac{\pi }{2}} \right) = 0\\ \Rightarrow 5\pi t – \frac{\pi }{2} = \frac{\pi }{2} + k\pi \Rightarrow t = \frac{1}{5} + \frac{k}{5}\,\end{array}\)
với \(k = – 1,0,1,2….\)
+ Thời điểm vật có li độ \(x = 0,1m = 10cm\) là:
\(\begin{array}{l}20\cos \left( {5\pi t – \frac{\pi }{2}} \right) = 10 \Leftrightarrow \cos \left( {5\pi t – \frac{\pi }{2}} \right) = \frac{1}{2}\\ \Rightarrow \left\{ \begin{array}{l}5\pi t – \frac{\pi }{2} = \frac{\pi }{3} + k2\pi \\5\pi t – \frac{\pi }{2} = \frac{\pi }{3} + k2\pi \end{array} \right. \Rightarrow \left\{ \begin{array}{l}t = \frac{1}{6} + \frac{{2k}}{5}\,\left( {k = 0,1,2…} \right)\\t = \frac{{ – 1}}{{30}} + \frac{{2k}}{5}\left( {k = 0,1,2…} \right)\end{array} \right.\end{array}\)