Hướng dẫn giải I.11 Bài ôn tập cuối Chương 1 (trang 14, 15, 16) – SBT Vật lí 11 Kết nối tri thức. Gợi ý: Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)với.
Câu hỏi/Đề bài:
Hình I.2 mô tả sự biến thiên gia tốc theo thời gian của một vật dao động
điều hoà.
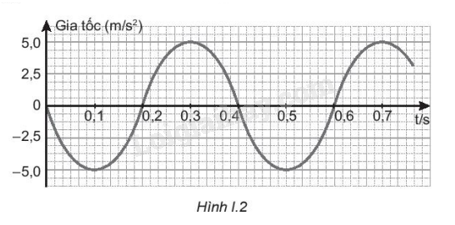
a) Viết phương trình gia tốc theo thời gian.
b) Viết phương trình li độ và vận tốc theo thời gian
Hướng dẫn:
Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)với:
+ \(x\) là li độ dao động.
+ \(A\) là biên độ dao động.
+ \(\omega \) là tần số góc của dao động.
+ \(\left( {\omega t + \varphi } \right)\) là pha của dao động ở thời điểm t.
+\(\varphi \) là pha ban đầu.
Phương trình của vận tốc có dạng : \(v = A\omega \cos \left( {\omega t + \varphi + \frac{\pi }{2}} \right)\)
- Khi vật ở VTCB : \(v = \pm \omega A\)
- Khi vật ở vị trí biên : \(v = 0\)
Phương trình của gia tốc có dạng : \(a = A{\omega ^2}\cos \left( {\omega t + \varphi + \pi } \right)\)
- Khi vật ở VTCB : \(a = 0\)
- Khi vật ở vị trí biên : \(a = \pm {\omega ^2}A\)
Lời giải chi tiết :
a) Dựa vào đồ thì ta có :
Tại t = 0 , \(a = – {\omega ^2}x = 0 = > x = 0\)=> Vật ở VTCB và vật chuyển động theo chiều dương => \({\varphi _0} = – \frac{\pi }{2}\)
Chu kì dao động \(T = 0,4s = > \omega = 5\pi (rad/s)\)
ð Phương trình của gia tốc : \(a = A{\omega ^2}\cos \left( {\omega t + \varphi + \pi } \right) = 5\cos \left( {5\pi t + \frac{\pi }{2}} \right)\)
b) Dựa vào đồ thị ta có :
Gia tốc cực đại : \(a = {\omega ^2}A = 5 = > A = \frac{5}{{{\omega ^2}}} = \frac{5}{{25{\pi ^2}}} = \frac{1}{{5{\pi ^2}}}(m) = 0,02m = 2cm\)
ð Phương trình dao động của vật : \(x = A\cos \left( {\omega t + \varphi } \right) = 2\cos \left( {5\pi t – \frac{\pi }{2}} \right)(cm)\)
ð Phương trình của vận tốc của vật : \(v = A\omega \cos \left( {\omega t + \varphi + \frac{\pi }{2}} \right) = 10\pi \cos \left( {5\pi t} \right)\left( {cm/s} \right)\)