Giải Câu 2.6 Bài 2. Mô tả dao động điều hòa (trang 6, 7) – SBT Vật lí 11 Kết nối tri thức. Gợi ý: Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà.
Câu hỏi/Đề bài:
Một chất điểm dao động điều hoà có phương trình li độ theo thời gian
\(x = 10\cos \left( {\frac{\pi }{3}t + \frac{\pi }{2}} \right)\left( {cm} \right)\). Tại thời điểm t vật có li độ 6 cm và đang hướng về vị trí cân bằng. Sau 9 s kể từ thời điểm t thì vật đi qua li độ:
A. 3 cm đang hướng về vị trí cân bằng.
B.\( – 3\) cm đang hướng về vị trí biên.
C. 6 cm đang hướng về vị trí biên.
D. \( – 6\) cm đang hướng về vị trí cân bằng.
Hướng dẫn:
Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)với:
+ \(x\) là li độ dao động.
+ \(A\) là biên độ dao động.
+ \(\omega \) là tần số góc của dao động.
+ \(\left( {\omega t + \varphi } \right)\) là pha của dao động ở thời điểm t.
+\(\varphi \) là pha ban đầu.
Chu kì: T là khoảng thời gian để vật thực hiện được một dao động.
Tần số: f là số dao động mà vật thực hiện được trong một giây \(f = \frac{1}{T}\)
Đơn vị của tần số là Héc (Kí hiệu Hz)
Tần số góc \(\omega = \frac{{2\pi }}{T} = 2\pi f(rad/s)\)
Lời giải:
:
Từ phương trình ta có :\(\omega = \frac{\pi }{3} = > T = \frac{{2\pi }}{\omega } = \frac{{2\pi .3}}{\pi } = 6(s)\)
Tại thời điểm t vật có li độ 6 cm và đang hướng về vị trí cân bằng
=> sau \(t = 9(s) = \frac{9}{6}T = 1,5T\) \( = T + \frac{T}{2}\) thì vật ở có li độ bằng -6 cm và đang hướng về VTCB
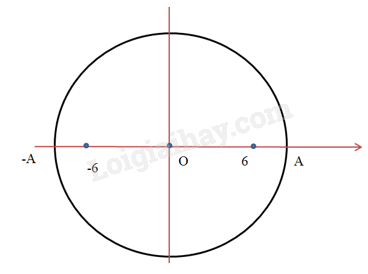
Đáp án :D