Giải Tự luận Bài 9. Sóng dừng (trang 34, 35, 36, 37, 38) – SBT Vật lí 11 Chân trời sáng tạo. Hướng dẫn: Áp dụng lí thuyết sóng dừng.
Câu hỏi/Đề bài:
9.1
Đề bài:
Một học sinh thực hiện thí nghiệm khảo sát sóng dừng với sóng âm hình thành trong các ống A, B, C, D đặt thẳng đứng, có đầu dưới kín, sóng âm được tạo ra bằng cách dùng một âm thoa đặt vào đầu trên để hở như Hình 9.4. Giả sử có sóng dừng trong ống tương ứng với chiều dài cực tiểu của ống.
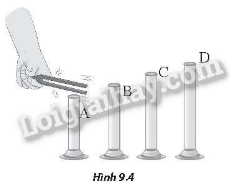
Hãy điền vào các chỗ trống trong bảng số liệu mà học sinh này thu nhận được.
|
Ống |
Chiều dài cột khí (cm) |
Bước sóng (cm) |
Tần số (Hz) |
Tốc độ sóng âm (m/s) |
|
A |
6,00 |
24,00 |
1 418,0 |
|
|
B |
12,00 |
48,00 |
708,0 |
|
|
C |
64,00 |
340,0 |
||
|
D |
20,00 |
425,0 |
Phương pháp giải
Áp dụng lí thuyết sóng dừng
Lời giải:
|
Ống |
Chiều dài cột khí (cm) |
Bước sóng (cm) |
Tần số (Hz) |
Tốc độ sóng âm (m/s) |
|
A |
6,00 |
24,00 |
1 418,0 |
340,3 |
|
B |
12,00 |
48,00 |
708,0 |
339,8 |
|
C |
16,00 |
64,00 |
531,3 |
340,0 |
|
D |
20,00 |
80,00 |
425,0 |
340,0 |
9.2
Đề bài:
Xét một sóng dừng trên dây có hai đầu cố định được hình thành từ dao động của sóng âm ở hoạ âm bậc ba. Tốc độ truyền sóng trên dây là 192 m/s và tần số sóng là 240 Hz. Biên độ dao động tại bụng sóng là 0,40 cm. Tính biên độ dao động của điểm M và N trên dây. Biết khoảng cách từ điểm M, N đến một đầu dây lần lượt là 40,0 cm và 20,0 cm.
Phương pháp giải
Áp dụng công thức tính bước sóng trong sóng dừng
Lời giải:
Ta có: \(\lambda = \frac{v}{f} = \frac{{192}}{{240}} = 80cm\)
Điểm M cách một đầu dây \(40cm = \frac{\lambda }{2}\)là một nút sóng nên đứng yên hay biên độ bằng 0.
Điểm N cách một đầu dây \(20cm = \frac{\lambda }{4}\)là một bụng sóng nên dao động với biên độ 0,40 cm.
9.3
Đề bài:
Cho biết phương trình dao động của một điểm M trên dây có hai đầu cố định khi có sóng dừng là uM=cos(0,50πt−0,20πx)(cm) (x được tính theo đơn vị cm và t được tính theo đơn vị s).
a) Tính tần số và bước sóng.
b) Tìm số bụng sóng và số nút sóng trên dây (kể cả hai đầu dây), cho biết dây có chiều dài bằng 50 cm.
Phương pháp giải
Dựa vào phương trình sóng dừng
Lời giải:
a) Ta có: 2πf=0,5π⇒f=0,25Hz
Ta có: \(\frac{{2\pi }}{\lambda } = 0,2\pi \Rightarrow \lambda = 10cm\)
b) Ta có: \(l = n\frac{\lambda }{2} \Rightarrow n = \frac{{2l}}{\lambda } = \frac{{2.50}}{{10}} = 10\). Trên dây có 10 bụng sóng và 11 nút sóng.
9.4
Đề bài:
Trên một dây đàn guitar có hình thành hệ sóng dừng với hai hoạ âm liên tiếp có tần số lần lượt là 280 Hz và 350 Hz.
a) Tần số 280 Hz tương ứng với hoạ âm bậc mấy?
b) Tìm tần số của hoạ âm bậc 1.
Phương pháp giải
Áp dụng công thức tính họa âm
Lời giải:
a) Ta có: \(\frac{{{f_n}}}{{{f_{n + 1}}}} = \frac{n}{{n + 1}} = \frac{{280}}{{350}} \Rightarrow n = 4\)
b) \({f_4} = 4{f_1} = 280Hz \Rightarrow {f_1} = 70Hz\)
9.5
Đề bài:
Tai của một người có thể được xem như một ống chứa không khí có chiều dài L, có một đầu bịt kín (màng nhĩ) và một đầu hở (Hình 9.5). Biết tốc độ âm thanh trong không khí là 343 m/s.
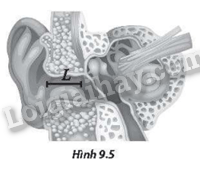
a) Tần số của âm cơ bản mà tai người này nghe được là 3,60 kHz. Tính bước sóng tương ứng với tần số này và chiều dài L của ống tai.
b) Tính tần số và bước sóng của hoạ âm bậc 3. Tai người này có nghe được hoạ âm này không?
Phương pháp giải
Áp dụng điều kiện có sóng dừng
Lời giải:
a) Bước sóng của sóng âm đang xét\({\lambda _1} = \frac{v}{{{f_1}}} = \frac{{343}}{{3,{{6.10}^3}}} = 9,53cm\)
Điều kiện có sóng dừng: \(L = \frac{{{\lambda _1}}}{4} = 2,38cm\)
b) Tần số và bước sóng của hoạ âm bậc 3 là:
\({f_3} = 3{f_1} = 3.3,6 = 10,8kHz;{\lambda _3} = \frac{v}{{{f_3}}} = \frac{{343}}{{10,{{8.10}^3}}} = 3,18cm\)
Tai người nghe được hoạ âm bậc 3 .
9.6
Đề bài:
Thực hiện thí nghiệm khảo sát sóng dừng như Hình 9.6, OA là một dây đàn hồi, với đầu O được gắn vào một nhánh của âm thoa dao động với biên độ đủ nhỏ để có thể xem như là một nút sóng. Sóng được tạo ra trên dây có tần số bằng 0,50 Hz. Dây xuyên qua đĩa tròn D tại điểm M, đĩa D có thể dịch chuyển lên hoặc xuống.
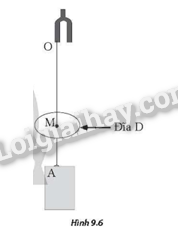
a) Khi dịch chuyển, đĩa D đóng vai trò gì trong sự hình thành sóng dừng?
b) Khi OM = 50,0cm, ta quan sát thấy có một bụng sóng trên dây. Tính tốc độ truyền sóng.
c) Với tốc độ truyền sóng như ở câu b), đĩa D phải dịch chuyển một khoảng nhỏ nhất bằng bao nhiêu để lại có sóng dừng xuất hiện trên dây?
Phương pháp giải
Điều kiện để có sóng dừng trên dây có hai đầu cố định
Lời giải:
a) D đóng vai trò là vật cản cố định để phản xạ sóng. Khi D dịch chuyển, chiều dài dây thay đổi để thoả mãn điều kiện có sóng dừng trên dây.
b) Điều kiện để có sóng dừng trên dây có hai đầu cố định: \(OM = \frac{\lambda }{2} = \frac{v}{{2f}}\)
=> v=2.0,50.50,0=50,0 cm/s
c) Dựa vào điều kiện để có sóng dừng trên dây có hai đầu cố định:
\(OM’ = 2\frac{\lambda }{2} = 2\frac{v}{{2f}} = 1m\)
9.7
Đề bài:
Quan sát một hệ sóng dừng trên dây đàn hồi, ta thấy với M là một nút sóng và N là bụng sóng kế cận thì khoảng cách . Cho biết bề rộng của một bụng sóng là 4 cm. Tìm biên độ dao động của sóng và biên độ dao động của điểm I là trung điểm của MN.
Phương pháp giải
Áp dụng công thức tính biên độ sóng
Lời giải:
Vì biên độ dao động tại bụng sóng là 2a nên bề rộng bụng sóng là 4a.
Suy ra biên độ sóng: \(a = \frac{4}{4} = 1cm\)
Biên độ dao động của I là trung điểm của MN:
\({a_1} = 2a\sin \frac{{2\pi d}}{\lambda } = 2.1.\sin \frac{{2\pi \frac{\lambda }{8}}}{\lambda } = 1,4cm\)
9.8
Đề bài:
Trong một lò vi sóng, khi hệ sóng dừng của sóng điện từ hình thành, người ta đo được khoảng cách giữa hai vị trí nóng nhất trên đĩa đặt trong lò là 6,40 cm. Cho biết tốc độ của sóng điện từ trong chân không là 3.108 m/s. Tính tần số của sóng điện từ sử dụng trong lò và giải thích cụm từ “vi sóng”.
Phương pháp giải
Áp dụng công thức tính khoảng cách giữa hai bụng sóng
Lời giải:
Khoảng cách giữa hai vị trí nóng nhất trên đĩa là khoảng cách giữa hai bụng sóng: \(d = \frac{\lambda }{2} = \frac{c}{{2f}} \Rightarrow f = \frac{c}{{2d}} = \frac{{{{3.10}^8}}}{{2.6,{{4.10}^{ – 2}}}} \approx 2,{34.10^9}Hz\)
Do bước sóng của sóng điện từ được sử dụng trong lò là λ=12,8 cm tương ứng sóng vô tuyến có bước sóng nhỏ (vi sóng).
9.9
Đề bài:
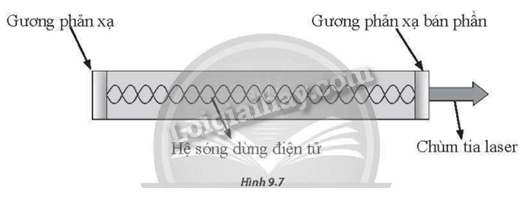
Để chế tạo tia laser, người ta sử dụng hốc quang học (optical cavity): sóng điện từ được phản xạ qua lại nhiều lần giữa hai gương (trong đó có một gương phản xạ bán phần để chùm tia laser lọt ra ngoài). Hai gương này được xem là hai đầu phản xạ cố định. Trong hốc quang học xuất hiện hiện tượng sóng dừng của sóng điện từ (Hình 9.7). Biết tia laser helium-neon có bước sóng 632,992 nm (màu đỏ) và khoảng cách giữa hai gương là 310,372 nm.
a) Có bao nhiêu nút sóng hình thành trong hốc quang học?
b) Tìm giá trị lớn nhất của bước sóng λ và gần nhất với giá trị 632,992 nm để có thể hình thành hệ sóng dừng trong hốc quang học này.
Phương pháp giải
Áp dụng điều kiện có sóng dừng
Lời giải:
a) Ta có: \(L = n\frac{\lambda }{2} \Rightarrow n = \frac{{2L}}{\lambda } = \frac{{2.210,{{372.10}^{ – 3}}}}{{632,{{992.10}^{ – 9}}}} \approx 980650,62\)
Suy ra: có 980651 nút sóng (kể cả hai nút sóng tại hai gương).
b) Theo yêu cầu bài toán, sóng điện từ mới sẽ tạo ra sóng dừng có số nút giảm đi 2 nút (1 bó sóng), do đó ta có:
\(\lambda ‘ = \frac{{2L}}{{n’}} = \frac{{2.210,{{372.10}^{ – 3}}}}{{980649}} \approx 632,993mm\), gần nhất với giá trị của bước sóng cũ