Đáp án Tự luận Bài 8. Giao thoa sóng (trang 29, 30, 31, 32, 33) – SBT Vật lí 11 Chân trời sáng tạo. Gợi ý: Áp dụng điều kiện cực đại giao thoa.
Câu hỏi/Đề bài:
8.1
Đề bài:
Trong hiện tượng giao thoa sóng nước do hai nguồn kết hợp A và B dao động cùng pha tạo ra trên cùng một dãy gồm những điểm dao động với biên độ cực đại, xét điểm M cách A và B các khoảng bằng 21 cm, 19 cm và điểm N cách A một khoảng 24 cm. Tỉnh khoảng cách từ N đến B.
Phương pháp giải
Áp dụng điều kiện cực đại giao thoa
Lời giải:
Ta có điều kiện cực đại giao thoa: MA−MB=kλ=NA−NB. (do M và N thuộc dùng một dãy)
=> NB=NA−(MA−MB)=24−(21-19)=22 cm
8.2
Đề bài:
Trong thí nghiệm Young về giao thoa của ánh sáng đơn sắc, hai khe hẹp cách nhau 1,2 mm, mặt phẳng chứa hai khe cách màn quan sát là 1,5 m. Khoảng cách giữa 5 vân sáng liên tiếp là 3,6 mm. Bước sóng của ánh sáng dùng trong thí nghiệm này bằng bao nhiêu?
Phương pháp giải
Áp dụng công thức tính khoảng vân
Lời giải:
Ta có: \(4i = 4\frac{{\lambda D}}{a} = 4\frac{{\lambda .1,5}}{{1,{{2.10}^{ – 3}}}} = 3,{6.10^{ – 3}} \Rightarrow \lambda = 720nm\)
8.3
Đề bài:
Khi thực hiện thí nghiệm Young về giao thoa ánh sáng với ánh sáng đơn sắc có bước sóng 560 nm, ta thấy khoảng cách giữa vân sáng bậc hai và vận tối thứ năm kể từ vẫn trung tâm và cùng phía với vân trung tâm là 3 mm. Cho biết khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 1,2 m. Tỉnh khoảng cách giữa hai khe
Phương pháp giải
Áp dụng công thức tính khoảng vân
Lời giải:
Ta có: \(4,5i – 2i = 2,5\frac{{\lambda D}}{a} = 2,5\frac{{{{560.10}^{ – 9}}.1,2}}{a} = {3.10^{ – 3}} \Rightarrow a = 0,56mm\)
8.4
Đề bài:
Trên mặt nước có sự giao thoa của hai sóng do hai nguồn kết hợp A và B dao động cùng pha, cùng biên độ tạo ra. Gọi A là bước sóng của sóng do hai nguồn phát ra. Xét một điểm nằm trong vùng giao thoa trên dãy đứng yên thứ ba kể từ đường trung trực của đoạn AB, xác định hiện khoảng cách từ điểm này đến hai nguồn A và B.
Phương pháp giải
Áp dụng điều kiện cực tiểu giao thoa
Lời giải:
M cách A và B cách khoảng MA và MB sao cho thoả mãn điều kiện cực tiểu giao thoa:
\(MA – MB = \left( {k + \frac{1}{2}} \right)\lambda = \frac{\lambda }{2};\frac{{3\lambda }}{2};\frac{{5\lambda }}{2};…\)
Vân đứng yên thứ ba tương ứng với k=2 =>\(MA – MB = \frac{{5\lambda }}{2}\)
8.5
Đề bài:
Trong hiện tượng giao thoa sóng trên mặt nước do hai nguồn kết hợp A và B cùng pha, cùng tần số bằng 24 Hz gây ra. Tại một điểm M trong vùng giao thoa trên mặt nước, ta quan sát thấy sóng có biên độ cực đại và là dãy cực đại thứ ba kể từ cực đại trung tâm. Phải thay đổi tần số sóng bằng bao nhiêu để tại M có
a) Dãy cực đại bậc bốn kể từ cực đại trung tâm?
b) Dãy đứng yên thứ ba kể từ cực đại trung tâm?
Phương pháp giải
Áp dụng điều kiện cực đại giao thoa
Lời giải:
a) Để thay đổi từ dãy cực đại bậc ba thành dãy cực đại bậc bốn kể từ đường trung trực của AB thì MA−MB= 3λ1= 4λ2
\( \Rightarrow 3\frac{v}{{{f_1}}} = 4\frac{v}{{{f_2}}}\)
Từ đó suy ra: \({f_2} = \frac{4}{3}{f_1} = 32Hz\)
b) Để thay đổi từ dãy cực đại bậc ba thành dãy đứng yên thứ ba kể từ đường trung trực của AB thì MA−MB= 3λ1= 2,5λ2
\( \Rightarrow 3\frac{v}{{{f_1}}} = 2,5\frac{v}{{{f_3}}}\)
Từ đó suy ra: \({f_3} = \frac{{2,5}}{3}{f_1} = 20Hz\)
8.6
Đề bài:
Trong thí nghiệm giao thoa sóng trên mặt nước, hai nguồn sóng A và B dao động với phương trình u=a=5cos10πt (cm). Biết tốc độ truyền sóng là 20 cm/s.
a) Viết phương trình dao động của điểm M trên mặt nước cách A, B lần lượt 7,2 cm và 8,2 cm.
b) Một điểm N trên mặt nước có AN -BN=10 cm. Điểm N nằm trên dãy gồm những điểm dao động với biên độ cực đại hay đứng yên?
Phương pháp giải
Sử dụng phương trình giao thoa
Lời giải:
a) Ta có: \(\lambda = \frac{{20}}{5} = 4cm\)
\({u_M} = {u_1} + {u_2} = A\cos \left( {\omega t – \frac{{2\pi {x_1}}}{\lambda }} \right) + A\cos \left( {\omega t – \frac{{2\pi {x_2}}}{\lambda }} \right) = 2A\cos \pi \frac{{{x_1} – {x_2}}}{\lambda }\cos \left( {\omega t – \pi \frac{{{x_1} + {x_2}}}{\lambda }} \right) = 5\sqrt 2 \cos (10\pi t – 3,85\pi )cm\) b) AN – BN =10 cm = 2,5 λ: N nằm trên dãy đứng yên thứ ba kể từ cực đại trung tâm, gần phía A hơn
8.7
Đề bài:
Trong thí nghiệm giao thoa sóng trên mặt nước, hai nguồn sóng kết hợp cùng pha đặt tại hai điểm A và B cách nhau 30 cm. Xét điểm M nằm trên đoạn AB và cách A 20 cm, điểm N nằm trên mặt nước và cách M 40 cm, MN vuông góc với AB (Hình 8,2)
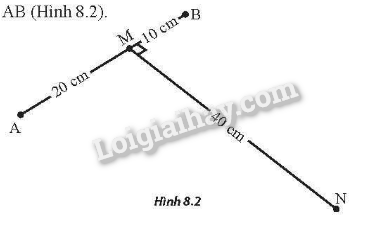
a) Với tần số của hai nguồn bằng 10 Hz thì tại N có sóng với biên độ cực đại và giữa N với đường trung trực của AB không có dãy cực đại. Tính tốc độ truyền sóng.
b) Với tốc độ truyền sóng tỉnh được ở câu a), để điểm N đứng yên thì tần số của hai nguồn phải bằng bao nhiêu?
Phương pháp giải
Áp dụng điều kiện cực đại giao thoa
Lời giải:
a) Theo đề bài, N nằm ở dãy cực đại bậc một kể từ cực đại trung tâm. Do đó:
NA−NB=kλ
\( \Rightarrow \sqrt {{{20}^2} + {{40}^2}} – \sqrt {{{10}^2} + {{40}^2}} = 1.\frac{v}{{10}} \Rightarrow v = 35cm/s\)
b) Để điểm N đứng yên thì N phải nằm trên dãy cực tiểu:
\(NA – NB = \left( {k + \frac{1}{2}} \right)\lambda = \left( {k + \frac{1}{2}} \right)\frac{{35}}{f} \Rightarrow f = 5Hz\)
8.8
Đề bài:
Trong thí nghiệm giao thoa sóng trên mặt nước với hai nguồn kết hợp A và B dao động cùng pha, tốc độ truyền sóng là 0,5 m/s, tần số sóng là 25 Hz.
a) Trong vùng không gian giữa hai nguồn, có bao nhiêu đây gồm những điểm dao động với biên độ cực đại và bao nhiêu dãy gồm những điểm đứng yên? Cho biết hai nguồn cách nhau 13 cm.
b) Tính khoảng cách giữa hai điểm liên tiếp trên đoạn AB dao động với biên độ cực đại và khoảng cách giữa hai điểm liên tiếp đứng yên
c) Khoảng cách giữa một điểm dao động với biên độ cực đại và một điểm đứng yên kế cận trên đoạn AB bằng bao nhiêu?
Phương pháp giải
Áp dụng điều kiện cực đại giao thoa
Lời giải:
a) Ta có: \(\lambda = \frac{{50}}{{25}} = 2cm\)
Gọi M là một điểm dao động cực đại trên AB
MA – MB = kλ (1)
MA + MB = AB (2)
Từ (1) và (2) \( \Rightarrow MA = \frac{{k\lambda }}{2} + \frac{{AB}}{2}\)
Vì 0<MA<AB\( \Rightarrow – \frac{{AB}}{\lambda } < k < \frac{{AB}}{\lambda } \Rightarrow – 6,5 < k < 6,5\)
=> k = 0, ±1,±2,±3,±4,±5,±6
Có 13 dãy gồm những điểm dao động với biên độ cực đại
=> Tương tự, với những điểm đứng yên: -7 < k < 6
=> k = 0, ±1,±2,±3,±4,±5,±6
b) Gọi M1 và M2 là hai điểm liên tiếp trên AB dao động với biên độ cực đại với M1A > M2A: \({M_1}A – {M_2}A = k\frac{\lambda }{2} + \frac{{AB}}{2} – ((k – 1)\frac{\lambda }{2} + \frac{{AB}}{2}) = \frac{\lambda }{2} = 1cm\)
Tương tự, khoảng cách giữa hai điểm liên tiếp đứng yên trên AB cũng bằng 1,0 cm
c) Khoảng cách giữa một điểm dao động với biên độ cực đại và một điểm đứng yên kề cận là \(\frac{\lambda }{4} = 0,5cm\)
8.9
Đề bài:
Trong thí nghiệm Young về giao thoa ánh sáng, biết khoảng cách giữa hai khe là 0,40 mm và khoảng cách từ hai khe đến màn quan sát là 1,00 m. Khi ta dùng ánh sáng đơn sắc có bước sóng λ1 thì quan sát thấy trên một khoảng trong vùng giao thoa có chứa 7 vẫn sáng với khoảng cách giữa hai vân sáng ngoài cùng bằng 9,00 mm
a) Tính bước sóng λ1
b) Sử dụng nguồn sáng gồm hai ánh sáng đơn sắc có bước sóng λ1, và λ2, với λ2 = 400 nm. Xác định vị trí trên màn có vân sáng cùng màu với vân trung tâm và gần vân trung tâm nhất.
Phương pháp giải
Áp dụng công thức tính khoảng vân
Lời giải:
a) Ta có: \(6i = 6\frac{{\lambda D}}{a} \Rightarrow 6\frac{{{\lambda _1}.1}}{{0,{{4.10}^{ – 3}}}} = {9.10^{ – 3}} \Rightarrow {\lambda _1} = 600nm\)
b) Tại vân trung tâm hai ánh sáng đơn sắc λ1 và λ2 cho vân sáng trùng nhau nên vân trung tâm có màu hỗn hợp của hai ánh sáng đơn sắc. Vị trí vân cùng màu với vân trung tâm là vị trí hai vân sáng tương ứng của λ1 và λ2 trùng nhau: \({k_1}\frac{{{\lambda _1}D}}{a} = {k_2}\frac{{{\lambda _2}D}}{a} \Rightarrow {k_1}{\lambda _1} = {k_2}{\lambda _2} \Rightarrow {k_1} = \frac{{400}}{{600}}{k_2}\)
Vì k1 và k2 là số nguyên nên giá trị của k1, k2 là:
k1=±2,±4,±6,…
k2=±3,±6,±9,…
Vị trí vân cùng màu và gần vân trung tâm nhất tương ứng với
k1=±2
k2=±3: x1=x2k1i1=k2i2=±3 mm ( ở hai phía so với vân trung tâm)
8.10
Đề bài:
Trong thí nghiệm Young về giao thoa ánh sáng, hai khe được chiếu bởi ánh sáng đơn sắc có bước sóng là 600 nm. Biết khoảng cách giữa hai khe là 1,20 mm và khoảng cách tử mặt phẳng chứa hai khe đến màn quan sát là 2,00 m.
a) Tại các điểm M và N trên màn, M, N cùng phía so với vân trung tâm cách vẫn trung tâm các khoảng lần lượt là 6,00 mm và 9,5 mm có vân sáng hay vân tối?
b) Không kể các vân tại M và N, trong khoảng giữa M. N có bao nhiêu vân sáng và bao nhiêu vận tối
Phương pháp giải
Áp dụng công thức tính khoảng vân
Lời giải:
a) Ta có: \(i = \frac{{{{600.10}^{ – 9}}.2}}{{1,{{2.10}^{ – 3}}}} = 1mm\)
\(\frac{{{x_M}}}{i} = 6\) tại M có vân sáng bậc sáu
\(\frac{{{x_N}}}{i} = 9,5\)tại N có vân tối thứ mười
b) Không kể các vân M và N, trong khoảng giữa M, N có ba vân sáng ( bậc 7, 8, 9) và ba vân tối ( thứ 7, 8, 9)
8.11
Đề bài:
Trong thí nghiệm Young về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng trắng có bước sóng trong khoảng từ 400 nm đến 760 nm Biết khoảng cách giữa hai khe là 0,30 mm, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là 2,00 m.
a) Tính khoảng cách từ vân sáng bậc một màu đỏ đến vân sáng bậc một màu tìm ở cùng phía so với vân trung tâm. Khoảng giữa hai vân sáng này có màu gì?
b) Tỉnh khoảng cách từ vân sáng bậc hai màu đỏ đến vân sáng bậc hai màu tím ở cùng phía so với vận trung tâm. Trong khoảng giữa hai vân sáng này có xuất hiện dải màu cầu vồng không?
Phương pháp giải
Áp dụng công thức tính khoảng vân
Lời giải:
a) \({x_{d1}} – {x_{t1}} = 1\frac{{{\lambda _d}D}}{a} – 1\frac{{{\lambda _t}D}}{a} = 2,4mm\)
Trong khoảng giữa vân sáng bậc một màu đỏ và vân sáng bậc một màu tím là dải màu biến thiên liên tục từ đỏ đến tím.
b) \({x_{d2}} – {x_{t2}} = 2\frac{{{\lambda _d}D}}{a} – 2\frac{{{\lambda _t}D}}{a} = 2({x_{d1}} – {x_{t1}}) = 4,8mm\)
\({x_{t3}} = 3\frac{{{\lambda _t}D}}{a} = 8mm\)
\({x_{d2}} = 2\frac{{{\lambda _d}D}}{a} = 10,13mm\)
xt3 > xđ2 => vân sáng bậc ba màu tím nằm trong vùng quang phổ bậc hai nên vùng quang phổ bậc hai này không có dải màu biến thiên liên tục từ đỏ đến tím
8.12
Đề bài:
Trong thí nghiệm Young về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng trắng có bước sóng trong khoảng từ 400 năm đến 750 nm Những ánh sáng đơn sắc nào cho vân sáng tại vị trí vân sáng bậc bốn của ảnh sáng đó
Phương pháp giải
Áp dụng công thức tính khoảng vân
Lời giải:
Ta có: \({x_{d4}} = 4\frac{{{\lambda _d}D}}{a}\)
\({x_s} = k\frac{{\lambda D}}{a}\)
Các ánh sáng đơn sắc khác có vân sáng tại vị trí này khi 4λđ = kλ
Mà 400≤λ => 4 k = 5, 6, 7
Ba ánh sáng đơn sắc khác cho vân sáng trùng lên vân sáng bậc bốn của ánh sáng đỏ, có bước sóng lần lượt là: 429 nm, 500nm, 600nm.