Hướng dẫn giải Tự luận Bài 2. Phương trình dao động điều hòa (trang 9, 10, 11, 12, 13) – SBT Vật lí 11 Chân trời sáng tạo. Tham khảo: Dựa vào đồ thị đọc giá trị.
Câu hỏi/Đề bài:
2.1
Đề bài:
Một vật dao động điều hoả có đồ thị li độ – thời gian như Hình 2.2.Hãy xác định biên độ dao động của vật
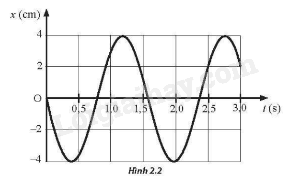
Hướng dẫn:
Dựa vào đồ thị đọc giá trị
Lời giải:
Biên độ dao động A= 4cm
2.2
Đề bài:
Một vật dao động điều hòa có phương trình là độ x=10cos(2t +π ) (cm). Hãy xác định biên độ, tần số góc, pha ban đầu của dao động.
Hướng dẫn:
Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + {\varphi _0}} \right)\)với:
+ \(x\) là li độ dao động.
+ \(A\) là biên độ dao động.
+ \(\omega \) là tần số góc của dao động.
+ \(\left( {\omega t + {\varphi _0}} \right)\) là pha của dao động ở thời điểm t.
+\({\varphi _0}\) là pha ban đầu.
Lời giải:
Biên độ dao động: A = 10 cm
Tần số góc: ω=2rad/s
Pha ban đầu: π rad
2.3
Đề bài:
Phương trình li độ của một chất điểm dao động điều hoà có dạng là x=Acos(ωt+π). Hãy xác định vị trí của vật tại thời điểm ban đầu
Hướng dẫn:
Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + {\varphi _0}} \right)\)với:
+ \(x\) là li độ dao động.
+ \(A\) là biên độ dao động.
+ \(\omega \) là tần số góc của dao động.
+ \(\left( {\omega t + {\varphi _0}} \right)\) là pha của dao động ở thời điểm t.
+\({\varphi _0}\) là pha ban đầu.
Lời giải:
Tại thời điểm ban đầu t = 0
x=Acos(0+π) = -A => vật ở biên âm
2.4
Đề bài:
Một con lắc là xo gồm vật nặng có khối lượng 200 g gắn vào là xo có độ cứng 50 N/m. Con lắc dao động điều hoà với biên độ 5 cm. Biết lần số góc của con lắc lò xo được xác định bởi biểu thức \(\omega = \sqrt {\frac{k}{m}} \), trong đó m là khối lượng của vật nặng, k là độ cứng của lò xo. Xác định gia tốc cực đại của vật
Hướng dẫn:
Áp dụng công thức tính gia tốc cực đại của vật: amax=ω2A
Lời giải:
Ta có: \(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{50}}{{0,2}}} = 5\sqrt {10} rad/s\)
Gia tốc cực đại của vật: amax=ω2A=5.(\(5\sqrt {10} \))2=1250 cm/s2
2.5
Đề bài:
Một vật dao động điều hoa có phương trình vận tốc là v=18cos(2t+π) (cm/s). Hãy xác định li độ của vật tại thời điểm \(t = \frac{\pi }{3}s\)
Hướng dẫn:
Thay giá trị của t vào phương trình của x để xác định li độ
Lời giải:
Phương trình li độ của vật: \(x = 9\cos \left( {2t + \frac{\pi }{2}} \right)cm\)
Li độ của vật tại thời điểm \(t = \frac{\pi }{3}s\)
\(x = 9\cos \left( {2.\frac{\pi }{3} + \frac{\pi }{2}} \right) = – \frac{{9\sqrt 3 }}{2}cm\)
2.6
Đề bài:
Một con lắc lò xo gồm một vật nhỏ có khối lượng bằng 200 g gắn vào lò xo có độ cứng 200 N/m có thể thực hiện dao động trên một mặt phẳng có ma sát không đáng kể. Kích thích để vật dao động điều hòa quanh vị trí cân bằng. Biết rằng trong khoảng thời gian 0,4 s vật đi được tổng quãng đường bằng 80 cm. Tính biên độ dao động của vật. Biết tần số góc của con lắc lò xo được xác định bởi biểu thức \(\omega = \sqrt {\frac{k}{m}} \), trong đó m là khối lượng của vật nặng, k là độ cứng của lò xo. Lấy π2 = 10
Hướng dẫn:
Dựa vào công thức tính tần số góc suy ra chu kì
Lời giải:
Ta có: \(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{200}}{{0,2}}} = 10\sqrt {10} rad/s\)
\(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{10\pi }} = 0,2s\)
Vì ∆t=2T => s = 8A\( \Rightarrow A = \frac{s}{8} = \frac{{80}}{8} = 10cm\)
2.7
Đề bài:
Một vật dao động điều hoà với biên độ 6 cm, tần số 25 Hz. Chọn gốc thời gian là lúc vật có li độ 33 cm và chuyển động cùng chiều với chiều dương đã chọn. Viết phương trình li độ của vật dao động.
Hướng dẫn:
Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà. Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + {\varphi _0}} \right)\)với:
+ \(x\) là li độ dao động.
+ \(A\) là biên độ dao động.
+ \(\omega \) là tần số góc của dao động.
+ \(\left( {\omega t + {\varphi _0}} \right)\) là pha của dao động ở thời điểm t.
+\({\varphi _0}\) là pha ban đầu.
Lời giải:
Ta có ω=2πf=2π.25=50π rad/s
Tại thời điểm ban đầu t = 0, ta có
x(0)=Acosφ0
\( \Rightarrow \cos {\varphi _0} = \frac{{3\sqrt 3 }}{6} = \frac{{\sqrt 3 }}{2}\) (1)
v(0) >0 => sinφ0 < 0 (2)
Từ 1 và 2 \( \Rightarrow \sin {\varphi _0} = – \frac{\pi }{6}rad\)
Phương trình li độ của vật dao động: \(x = 6\cos \left( {50\pi t – \frac{\pi }{6}} \right)cm\)
2.8
Đề bài:
Xét một con lắc lò xo đang dao động điều hoà với đô thị gia tốc — thời gian được thể hiện như Hình 2.3. Biết tần số góc của con lắc lò xo được xác định bởi biểu thức \(\omega = \sqrt {\frac{k}{m}} \), trong đó m là khối lượng của vật nặng, k là độ cứng của lò xo. Với lò xo được sử dụng có độ cứng là 100 N/m và lấy π2 = 10. Hãy xác định
a) Khối lượng của vật nặng.
b) Li độ của vật tại thời điểm t = 1,4 s
Hướng dẫn:
a) Từ công thức tính tốc độ góc suy ra khối lượng
b) Từ công thức tính gia tốc cực đại suy ra biên độ A
Lời giải:
a) Dựa vào đồ thị ta có: T = 1 s
\( \Rightarrow \omega = \frac{{2\pi }}{T} = \frac{{2\sqrt {10} }}{1} = 2\sqrt {10} rad/s\)
Khối lượng của vật nặng:
\(m = \frac{k}{{{\omega ^2}}} = \frac{{100}}{{4.10}} = 2,5kg\)
b) Dựa vào đồ thị ta có:
amax=0,4m/s2
=> ω2A=0,4
\( \Rightarrow A = \frac{{0,4}}{{{\omega ^2}}} = \frac{{0,4}}{{4.10}} = 0,01m\)
Tại thời điểm t = 0 s, gia tốc đạt giá trị cực tiểu => vật ở biên dương=> pha ban đầu của dao động là 0 rad
Phương trình li độ của vật: \(x = \cos (2\sqrt {10} t)cm\)
Li độ của vật tại thời điểm t = 1,4 s là: \(x = \cos (2\sqrt {10} .1,4) = – 0,84cm\)