Lời giải Tự luận Bài 18. Nguồn điện (trang 68, 69, 70, 71, 72) – SBT Vật lí 11 Chân trời sáng tạo. Tham khảo: Vận dụng định luật Ohm cho toàn mạch.
Câu hỏi/Đề bài:
18.1
Đề bài:
Mắc hai đầu điện trở 3Ω3Ω vào hai cực của một nguồn điện có suất điện động và điện trở trong lần lượt là E=6,0 V và r=1Ω
a) Tính cường độ dòng điện trong mạch.
b) Tính hiệu điện thế giữa hai đầu điện trở.
Phương pháp giải
Vận dụng định luật Ohm cho toàn mạch
Lời giải:
a) Áp dụng: \(I = \frac{{\rm{E}}}{{R + r}} = \frac{6}{{3 + 1}} = 1,5\;A\)
b) Áp dụng: \(U = RI = 3.1,5 = 4,5{\rm{\;V}}\)
18.2
Đề bài:
Mắc hai đầu điện trở R1 vào hai cực của một nguồn điện có suất điện động và điện trở trong lần lượt là E=8,0 V và r=2Ωthì dòng điện chạy qua điện trở có cường độ 1,6 A.
a) Tính R1.
b) Mắc thêm vào mạch một điện trở R2 song song với R1 thì dòng điện chạy qua R2 có cường độ \(\frac{2}{3}{\rm{A}}\). Tính R2.
Phương pháp giải
Vận dụng định luật Ohm cho toàn mạch
Lời giải:
a) Áp dụng: \(I = \frac{{\rm{E}}}{{{R_1} + r}} = \frac{8}{{{R_1} + 2}} = 1,6\;A \Rightarrow {R_1} = 3\Omega \)
b) R2 song song với R1 nên: \({R_1}{I_1} = {R_2}{I_2} \Rightarrow 3{I_1} = \frac{2}{3}{R_2} \Rightarrow {I_1} = \frac{2}{9}{R_2}\) và \(I = {I_1} + {I_2} = \frac{{2{R_2}}}{9} + \frac{2}{3} = \frac{8}{{2 + \frac{{3{R_2}}}{{{R_2} + 3}}}} \Rightarrow {R_2} = 6{\rm{\Omega }}\)
18.3
Đề bài:
Hai nguồn điện giống hệt nhau. Khi mắc hai đầu điện trở 3,2Ω vào hai cực một nguồn rồi sau đó mắc thêm nguồn còn lại theo cách cực dương của hai nguồn nối với nhau và cực âm hai nguồn nối với nhau thì thấy hiệu điện thế hai đầu điện trở tăng thêm 20% so với lúc đầu. Tính điện trở trong của mỗi nguồn.
Phương pháp giải
Vận dụng định luật Ohm cho toàn mạch
Lời giải:
Khi mắc thêm nguồn theo cách trên có nghĩa điện trở mắc vào bộ hai nguồn mắc song song. Vì hai nguồn giống hệt nhau nên: \({{\rm{E}}_b} = {\rm{E}};{r_b} = \frac{r}{2}\) Hiệu điện thế hai đầu điện trở tăng thêm 20%: \({U_2} = {U_1} + 0,2{U_1} = 1,2{U_1}\)
\(\left\{ {\begin{array}{*{20}{l}}{{U_1} = R{I_1} = \frac{{R{\rm{E}}}}{{R + r}}}\\{{U_2} = R{I_2} = \frac{{R{\rm{E}}}}{{R + \frac{r}{2}}}}\end{array} \Rightarrow \frac{{{U_2}}}{{{U_1}}} = \frac{{R + r}}{{R + \frac{r}{2}}} = 1,2} \right.\)
Thay R=3,2Ω, tính được r=1,6Ω.
18.4
Đề bài:
Hai nguồn điện giống hệt nhau được mắc thành bộ rồi nối hai cực của bộ nguồn với hai đầu của một điện trở thì kết quả là: cường độ dòng điện qua điện trở trong trường hợp hai nguồn mắc nối tiếp và hai nguồn mắc song song đều bằng nhau. Tính hiệu suất của bộ nguồn trong hai trường hợp.
Phương pháp giải
Vận dụng công thức mắc nguồn thành bộ
Lời giải:
Trường hợp hai nguồn mắc nối tiếp: \({I_1} = \frac{{{{\rm{E}}_{nt}}}}{{R + {r_{nt}}}} = \frac{{2{\rm{E}}}}{{R + 2r}}\)
Trường hợp hai nguồn mắc song song: \({I_2} = \frac{{{{\rm{E}}_{//}}}}{{R + {r_{//}}}} = \frac{{\rm{E}}}{{R + \frac{r}{2}}}\)
Từ (1) và (2) cho I1=I2 ta được R=r
Thay vào tính được hiệu suất tương ứng trong hai trường hợp:
\({H_1} = \frac{r}{{r + 2r}} = \frac{1}{3}\) và \({H_2} = \frac{r}{{r + \frac{r}{2}}} = \frac{2}{3}\)
18.5
Đề bài:
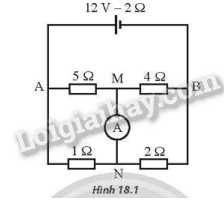
Cho mạch điện như Hình 18.1. Ampe kế A có điện trở không đáng kể.
a) Tìm số chỉ ampe kế và chiều dòng điện qua nó.
b) Đổi vị trí điện trở 5Ω5Ω và ampe kế A. Tìm số chỉ ampe kế và chiều dòng điện qua nó.
Phương pháp giải
Vận dụng định luật Ohm cho toàn mạch
Lời giải:
a) Vì điện trở ampe kế A bằng 0 nên UMN=0. Chập điểm M và N, mạch ngoài trở thành điện trở ((5Ω)//(1Ω)) nối tiếp với ((4Ω)//(2Ω))
Dòng điện trong mạch chính: \(I = \frac{{\rm{E}}}{{{R_N} + r}} = \frac{{12}}{{\frac{5}{6} + \frac{4}{3} + 2}} = 2,88A\)
Từ đó: \(\left\{ {\begin{array}{*{20}{l}}{{U_{{\rm{AM}}}} = {U_{{\rm{AN}}}} = 2,88.\frac{5}{6} = 2,4{\rm{\;V}}}\\{{U_{{\rm{AB}}}} = 2,88.\left( {\frac{5}{6} + \frac{4}{3}} \right) = 6,24{\rm{\;V}}}\end{array} \Rightarrow {U_{{\rm{MB}}}} = 6,24 – 2,4 = 3,84{\rm{\;V}}} \right.\)
Như vậy dòng điện qua điện trở 5Ω có chiều từ A đến M với cường độ: \(\frac{{2,4}}{5} = 0,48{\rm{\;A}}\)
Dòng điện qua điện trở 4Ω có chiều từ M đến B với cường độ: \(\frac{{3,84}}{4} = 0,96{\rm{\;A}}\)
Vậy dòng điện qua ampe kế A có chiều từ N đến M với cường độ: 0,96−0,48 = 0, 48A
b) Tương tự, lúc này điểm A chập với điểm M và ta có mạch gồm {((5Ω)//(1Ω))nt(2Ω)}//(4Ω). Tính được dòng điện trong mạch chính I=3,28 A; dòng điện qua điện trở 1Ω1Ω là 1,6 A và dòng điện qua ampe kế A bằng 3,28−1,6=1,68 A, có chiều từ A đến M.
18.6
Đề bài:
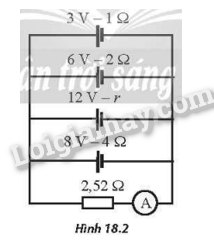
Cho mạch điện như Hình 18.2. Biết ampe kế lí tưởng A chỉ 1,92 A.
a) Tính điện trở trong r.
b) Đảo cực của nguồn (6 V−2Ω). Tìm lại số chỉ ampe kế.
Phương pháp giải
Vận dụng kiến thức mắc nguồn thành bộ
Lời giải:
Cách giải 1:
a) UAB=1,92.2,52=4,8384 V. Từ đó tính được dòng điện qua các nhánh:
Dòng điện I1 qua nguồn 3 V từ \({\rm{A}} \to {\rm{B}}:{I_1} = \frac{{4,8384 – 3}}{1} = 1,8384{\rm{\;A}}\)
Dòng điện I2 qua nguồn 6 V từ \({\rm{B}} \to {\rm{A}}:{I_2} = \frac{{6 – 4,8384}}{2} = 0,5808{\rm{\;A}}\)
Dòng điện I4 qua nguồn 8 V từ \({\rm{B}} \to {\rm{A}}:{I_4} = \frac{{8 – 4,8384}}{4} = 0,7904{\rm{\;A}}\)
Dòng điện I3 qua nguồn 12 V từ \({\rm{B}} \to {\rm{A}}:{I_3} + {I_2} + {I_4} = {I_1} + {I_{\rm{A}}} \Rightarrow {I_3} = 2,3872{\rm{\;A}}\)
Từ đó: \(r = \frac{{12 – 4,8384}}{{2,3872}} = 3{\rm{\Omega }}\)
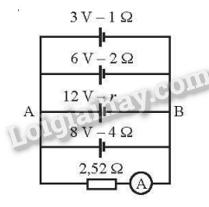
b) Đảo cực nguồn (6 V−2Ω), tính tương tự ta được: số chỉ ampe kế 0,96 A.
Cách giải 2:
a) Dùng phương pháp nguồn tương đương:
\(U = {{\rm{E}}_b} – {r_b}I \Rightarrow 2,52.1,92 = \frac{{\left( {\frac{3}{1} + \frac{6}{2} + \frac{{12}}{r} + \frac{8}{4}} \right)}}{{\frac{1}{1} + \frac{1}{2} + \frac{1}{r} + \frac{1}{4} – \frac{1}{1} + \frac{1}{2} + \frac{1}{r} + \frac{1}{4}}} \Rightarrow r = 3\Omega \)
b) Đảo cực nguồn (6 V−2Ω), tương tự ta được
\(I = \frac{{{{\rm{E}}_b}}}{{{r_b} + R}} = \frac{{{r_b}\left( {\frac{3}{1} + \frac{{ – 6}}{2} + \frac{{12}}{3} + \frac{8}{4}} \right)}}{{{r_b} + R}} = \frac{{0,48.\left( {\frac{3}{1} + \frac{{ – 6}}{2} + \frac{{12}}{3} + \frac{8}{4}} \right)}}{{0,48 + 2,52}} = 0,96\;A\)
18.7
Đề bài:
Có n nguồn điện không đổi giống nhau, mỗi nguồn có suất điện động E được mắc theo cách: Cực âm của nguồn thứ 1 nối với cực dương của nguồn thứ 2 ; cực âm của nguồn thứ 2 nối với cực dương của nguồn thứ 3 cực âm của nguồn thứ n nối với cực dương của nguồn thứ 1.
a) Tìm hiệu điện thế giữa hai cực của nguồn bất kì.
b) Đảo cực của một nguồn nào đó thì tỉ số hiệu điện thế giữa hai cực của nguồn này lớn gấp 40 lần hiệu điện thế giữa hai cực của một nguồn còn lại bất kì. Tính n.
Phương pháp giải
Vận dụng kiến thức mắc nguồn thành bộ
Lời giải:
Mỗi nguồn có suất điện động EE và điện trở trong r.
a) Cường độ dòng điện: \(I = \frac{{n{\rm{E}}}}{{nr}} = \frac{{\rm{E}}}{r}\)
Hiệu điện thế giữa hai cực của nguồn bất kì: \(U = {\rm{E}} – rI = {\rm{E}} – r\frac{{\rm{E}}}{r} = 0\)
b) Cường độ dòng điện: \(I = \frac{{\left( {n – 2} \right){\rm{E}}}}{{nr}}\)
Hiệu điện thế giữa hai cực nguồn đảo cực và một nguồn còn lại bất kì: \(\begin{array}{l}{U_{dao\,cuc}} = {\rm{E}} + rI = {\rm{E}} + r\frac{{\left( {n – 2} \right){\rm{E}}}}{{nr}} = \frac{{2{\rm{E}}\left( {n – 1} \right)}}{n}\\{U_{con\,lai}} = {\rm{E}} – rI = {\rm{E}} – r\frac{{\left( {n – 2} \right){\rm{E}}}}{{nr}} = \frac{{2{\rm{E}}}}{n} \Rightarrow \frac{{{U_{dao\,cuc}}}}{{{U_{con\,lai}}}} = \left( {n – 1} \right) = 40 \Rightarrow n = 41\end{array}\)
18.8
Đề bài:
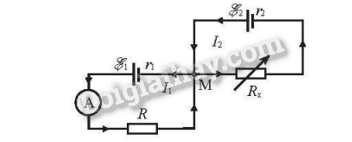
Cho mạch điện như Hình 18.3. Số chỉ ampe kế thay đổi như thế nào khi tăng dần biến trở Rx từ giá trị 0 .
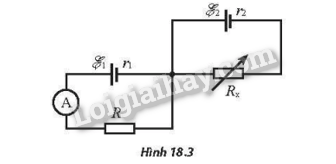
Phương pháp giải
Áp dụng định luật Ohm
Lời giải:
Áp dụng định luật Ohm cho mỗi vòng kín, ta có: \({I_1} = \frac{{{{\rm{E}}_1}}}{{R + {r_1}}};{I_2} = \frac{{\rm{E}}}{{{R_x} + {r_2}}}\). Như vậy số chỉ ampe kế A (dòng I1) không phụ thuộc vào giá trị Rx.
18.9
Đề bài:
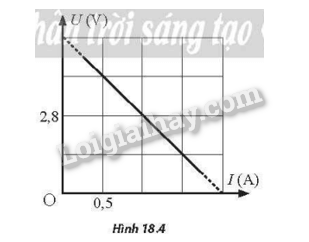
Trong việc thiết kế các mạch điện, để có được các suất điện động thích hợp người ta thường tiến hành ghép các nguồn có sẵn thành các bộ nguồn có suất điện động cần thiết. Xét bốn pin giống nhau được mắc nối tiếp thành bộ nguồn, rồi mắc hai đầu một biến trở vào hai đầu bộ nguồn thành mạch kín. Điều chỉnh giá trị biến trở, đồ thị biểu diễn sự phụ thuộc của điện áp hai đầu bộ nguồn U vào cường độ dòng điện I trong mạch như Hình 18.4. Tìm suất điện động và điện trở trong của mỗi pin.
Phương pháp giải
Áp dụng định luật Ohm
Lời giải:
Gọi suất điện động và điện trở trong mỗi nguồn là và r nên suất điện động và điện trở trong của bộ nguồn tương ứng là 4E và 4r.
Áp dụng định luật Ohm ⇒U=4E−4rI ta có đường biểu diễn U theo I là một đường thẳng.
Thay hai cặp điểm trên đồ thị, ta được: \(\left\{ {\begin{array}{*{20}{l}}{4,2 = 4{\rm{E}} – 4r.0,5}\\{2,8 = 4{\rm{E}} – 4r.1,0}\end{array}} \right.\)
Giải ra ta được: E=1,4V và r=0,7Ω.
18.10
Đề bài:
Người ta muốn tạo ra một điện trở R=3Ωbằng cách dùng một dây dẫn đồng chất có đường kính tiết tiết diện 1,0 mm, điện trở suất ρ=3⋅10−7Ωmcó bọc lớp cách điện rất mỏng quấn thành một lớp gồm N vòng sát nhau quanh hình trụ bằng sứ có đường kính tiết diện 2,0 cm.
a) Tính số vòng N.
b) Có một số bóng đèn gồm hai loại: loại (6 V−3 W) và loại (3 V−1 W) được mắc thành 5 dãy song song rồi mắc chúng nối tiếp với điện trở R=3Ωthành mạch điện. Đặt hai đầu mạch điện này vào một hiệu điện thế không đổi U=12 V. Biết tất cả các đèn đều sáng bình thường. Hãy xác định số lượng mỗi loại đèn. Coi điện trở của các đèn không thay đổi và bỏ qua điện trở của các dây nối.
Phương pháp giải
Vận dụng công thức tính điện trở và định luật Ohm
Lời giải:
a) \(R = \rho \frac{{4\ell }}{{\pi {d^2}}} = \rho \frac{{4N\pi D}}{{\pi {d^2}}} = \rho \frac{{4ND}}{{{d^2}}} \Rightarrow N = \frac{{R{d^2}}}{{4\rho D}} = \frac{{3.{{\left( {1,{{0.10}^{ – 3}}} \right)}^2}}}{{{{4.3.10}^{ – 7}}{{.2.10}^{ – 2}}}} = 125\)vòng
b) Khi các đèn sáng bình thường:
Dòng điện định mức của đèn (6 V−3 W) và đèn (3 V−1 W) lần lượt là
\({I_1} = \frac{{{{\rm{P}}_1}}}{{{U_1}}} = \frac{3}{6} = \frac{1}{2}\;A\) và \({I_2} = \frac{{{{\rm{P}}_2}}}{{{U_2}}} = \frac{1}{3}\;A\)
⇒⇒ Mỗi dãy chỉ gồm 1 đèn 6 V hoặc 2 đèn 3 V nối tiếp.
Dòng điện mạch chính: \(I = \frac{{12 – 6}}{3} = 2{\rm{\;A}}\). Gọi m là số dãy mắc đèn 6 V và n là số dãy mắc đèn 3 V.
Thiết lập phương trình: \(I = m{I_1} + n{I_2} \Rightarrow \frac{1}{2}m + \frac{1}{3}n = 2 \Rightarrow m = 2\) và n = 3 .
Vậy cần 2 bóng 6 V và 6 bóng 3 V.
18.11
Đề bài:
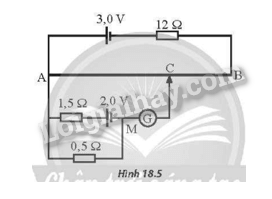
Một mạch chiết áp trong đó các giá trị suất điện động của pin và các điện trở được cho như Hình 18.5. Bỏ qua điện trở trong của các pin và của các dây nối. Đoạn AB là một dây thép đồng chất, tiết diện đều, chiều dài AB = 48cm và có điện trở 3Ω . G là một điện kế lí tưởng. Hãy tìm khoảng cách AC để kim điện kế chỉ số 0 .
Phương pháp giải
Áp dụng định luật Ohm cho toàn mạch
Lời giải:
Vì điện kế G chỉ số 0, nên không có dòng điện chạy qua đoạn MC (qua điện kế).
UMC=0⇒UAM=UAC (điểm M chập với điểm C).
Dòng điện qua AB do nguồn 3 V là: \({I_1} = \frac{3}{{12 + 3}} = 0,2{\rm{\;A}}\)
Dòng qua điện trở do nguồn 2 V là: \({I_2} = \frac{2}{{1,5 + 0,5}} = 1{\rm{\;A}}\)
\(\begin{array}{l} \Rightarrow {U_{{\rm{AM}}}} = {U_{{\rm{AC}}}} = 2 – 1,5 \cdot 1 = 0,5{\rm{\;V}} \Rightarrow {R_{{\rm{AC}}}} = \frac{{0,5}}{{0,2}} = 2,5{\rm{\Omega }}\\\frac{{{R_{{\rm{AC}}}}}}{{{R_{{\rm{AB}}}}}} = \frac{{{\rm{AC}}}}{{{\rm{AB}}}} \Rightarrow {\rm{AC}} = 40{\rm{\;cm}}\end{array}\)