Hướng dẫn giải Luyện tập 5 Bài 13. Hai mặt phẳng song song (trang 91, 92, 93) – SGK Toán 11 Kết nối tri thức. Tham khảo: Cách chứng minh lăng trụ.
Câu hỏi/Đề bài:
Cho hình lăng trụ tam giác ABC.A’B’C’. Gọi M và M’ lần lượt là trung điểm của các cạnh BC và B’C’. Chứng minh rằng AMC.A’M’C’ là hình lăng trụ.
Hướng dẫn:
Cách chứng minh lăng trụ
– Hai mặt đáy của lăng trụ song song nhau.
– Các mặt bên của hình lăng trụ là hình bình hành.
– Các cạnh bên song song, bằng nhau và tạo với đáy các góc bằng nhau.
Lời giải:
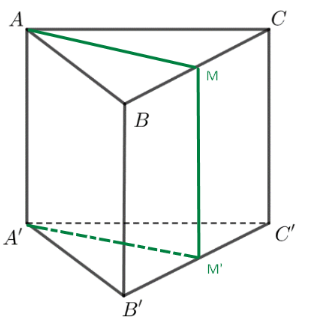
Ta có M, M’ lần lượt là trung điểm của BC, B’C’, BCC’B’ là hình bình hành suy ra MM’ // CC’.
Vì các cạnh bên của hình lăng trụ ABC.A’B’C’ đôi một song song nên AA’//CC’.
Mặt phẳng ((AMC) //(A’M’C’) nên AMC. AM’C’ là hình lăng trụ.