Giải Luyện tập 5 Bài 1. Giá trị lượng giác của góc lượng giác (trang 10) – SGK Toán 11 Kết nối tri thức. Hướng dẫn: Áp dụng \(\sin \alpha = y\) ; \(\cos \alpha = x\) ; \(\tan \alpha =\frac{y}{x}\) ; \(\cot \alpha =\frac{x}{y}\.
Câu hỏi/Đề bài:
Cho góc lượng giác có số đo bằng \(\frac{{5\pi }}{6}\)
a) Xác định điểm M trên đường tròn lượng giác biểu diễn góc lượng giác đã cho.
b) Tính các giá trị lượng giác của góc lượng giác đã cho.
Hướng dẫn:
Áp dụng \(\sin \alpha = y\) ; \(\cos \alpha = x\) ; \(\tan \alpha =\frac{y}{x}\) ; \(\cot \alpha =\frac{x}{y}\)
Lời giải:
a) Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó điểm M là điểm biểu diễn bởi góc có số đo \(\frac{{5\pi }}{6}\)
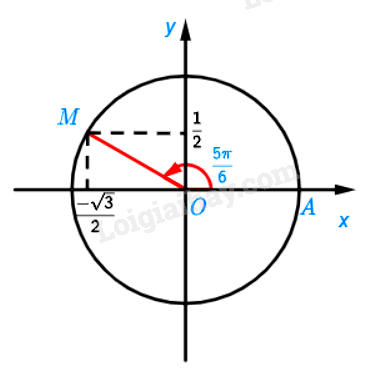
b) Ta có:
\(\sin \left( {\frac{{5\pi }}{6}} \right) = \frac{1}{2};\cos \left( {\frac{{5\pi }}{6}} \right) = \frac{{ – \sqrt 3 }}{2};\tan \left( {\frac{{5\pi }}{6}} \right) = \frac{{ – \sqrt 3 }}{3};\cot \left( {\frac{{5\pi }}{6}} \right) = \frac{{ – 3}}{{\sqrt 3 }}\)