Giải Luyện tập 4 Bài 1. Giá trị lượng giác của góc lượng giác (trang 10) – SGK Toán 11 Kết nối tri thức. Gợi ý: Đường tròn lượng giác có tâm tại gốc tọa độ, bán kính bằng 1, lấy điểm A(1.
Câu hỏi/Đề bài:
Xác định điểm M và N trên đường tròn lượng giác lần lượt biểu diễn các góc lượng giác có số đo bằng \( – \frac{{15\pi }}{4}\)và \({420^ \circ }\)
Hướng dẫn:
Đường tròn lượng giác có tâm tại gốc tọa độ, bán kính bằng 1, lấy điểm A(1;0) là gốc của đường tròn.
Điểm trên đường tròn lượng giác biểu diễn góc lượng giác có số đo là điểm M trên đường tròn lượng giác sao cho sđ\((OA,OM) = \alpha \)
Lời giải:
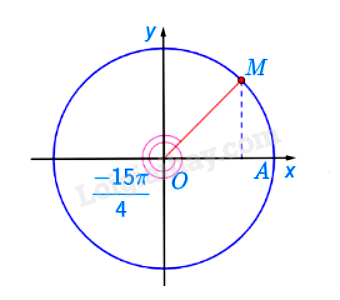
Điểm biểu diễn góc lượng giác có số đo bằng \( – \frac{{15\pi }}{4} = – \frac{{7\pi }}{4} + ( – 1).2\pi \) được xác định là điểm M.
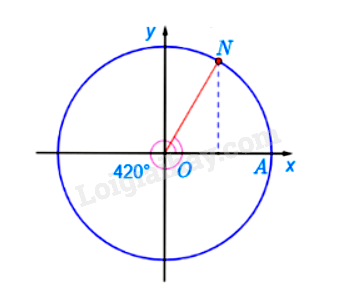
Ta có \(\frac{{420}}{{360}} = 1+ \frac{1}{6}\) Ta chia đường tròn thành 6 phần bằng nhau. Khi đó điểm N là điểm biểu diễn bởi góc có số đo \({420^ \circ }\)