Bài 7.41 trang 65 Toán 11 tập 2 – Kết nối tri thức: Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh bằng a. Biết tam giác SAD vuông cân tại S và (SAD) ⊥ (ABCD)

Đề bài/câu hỏi:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Biết tam giác SAD vuông cân tại \(S\) và \((SAD) \bot (ABCD)\).

a) Tính theo a thể tích của khối chóp S.ABCD.

b) Tính theo a khoảng cách giữa hai đường thẳng AD và SC.

Hướng dẫn:

– Thể tích khối chóp \(V = \frac{1}{3}h.S\)

– Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa một trong hai đường thẳng đó đến mặt phẳng song song với nó và chứa đường thẳng còn lại.

Lời giải:

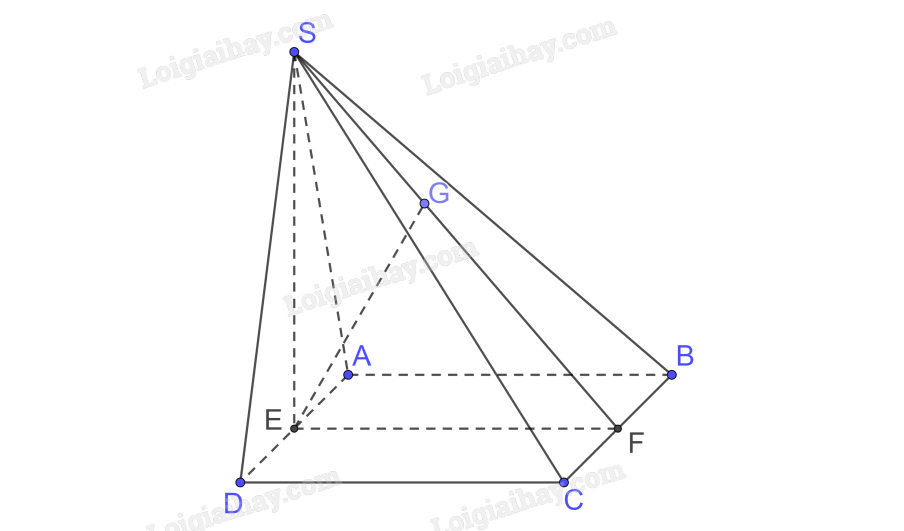
a) Trong (SAD) kẻ \(SE \bot AD\)

Mà \(\left( {SAD} \right) \bot \left( {ABCD} \right),\left( {SAD} \right) \cap \left( {ABCD} \right) = AD \Rightarrow SE \bot \left( {ABCD} \right)\)

Xét tam giác SAD vuông cân tại S có

\(SE \bot AD\)

\( \Rightarrow \) E là trung điểm của AD

\( \Rightarrow SE = \frac{{AD}}{2} = \frac{a}{2}\)

Diện tích hình vuông ABCD là \({S_{ABCD}} = {a^2}\)

Thể tích khối chóp là \(V = \frac{1}{3}SE.{S_{ABCD}} = \frac{1}{3}.\frac{a}{2}.{a^2} = \frac{{{a^3}}}{6}\)

b) Trong (ABCD) kẻ EF // AB mà \(AB \bot BC \Rightarrow EF \bot BC\)

mà \(SE \bot BC \Rightarrow BC \bot \left( {SEF} \right);BC \subset \left( {SBC} \right) \Rightarrow \left( {SEF} \right) \bot \left( {SBC} \right)\)

\(\left( {SEF} \right) \cap \left( {SBC} \right) = SF\)

Trong (SEF) kẻ \(EG \bot SF\)

\( \Rightarrow EG \bot \left( {SBC} \right)\)

Ta có AD // BC nên AD // (SBC)

\( \Rightarrow d\left( {AD,SC} \right) = d\left( {AD,\left( {SBC} \right)} \right) = d\left( {E,\left( {SBC} \right)} \right) = EG\)

Vì ABCD là hình vuông và EF // AB nên EF = AB = a

Xét tam giác SEF vuông tại E có

\(\frac{1}{{E{G^2}}} = \frac{1}{{S{E^2}}} + \frac{1}{{E{F^2}}} = \frac{1}{{{{\left( {\frac{a}{2}} \right)}^2}}} + \frac{1}{{{a^2}}} = \frac{5}{{{a^2}}} \Rightarrow EG = \frac{{a\sqrt 5 }}{5}\)

Vậy \(d\left( {AD,SC} \right) = \frac{{a\sqrt 5 }}{5}\)