Sử dụng định lí Pytago trong tam giác vuông. Giải và trình bày phương pháp giải Bài 7.13 trang 43 SGK Toán 11 tập 2 – Kết nối tri thức – Bài 24. Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng. Cho điểm S nằm ngoài mặt phẳng (P), có hình chiếu H trên (P)….
Đề bài/câu hỏi:
Cho điểm S nằm ngoài mặt phẳng (P), có hình chiếu H trên (P). Với mỗi điểm M bất kì (không trùng H) trên mặt phẳng (P), ta gọi đoạn thẳng SM là đường xiên, đoạn thẳng HM là hình chiếu trên (P) của đường xiên đó. Chứng minh rằng:
a) Hai đường xiên SM và SM’ bằng nhau khi và chỉ khi hai hình chiếu HM và HM’ tương ứng của chúng bằng nhau;
b) Đường xiên SM lớn hơn đường xiên SM’ nếu hình chiếu HM lớn hơn hình chiếu HM’.
Hướng dẫn:
Sử dụng định lí Pytago trong tam giác vuông.
Lời giải:
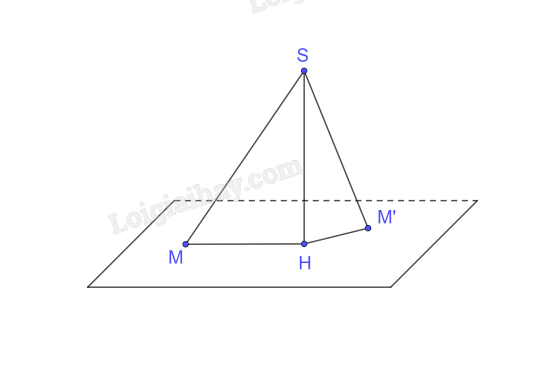
a)
+) Giả sử SM = SM’
Xét tam giác SHM vuông tại H có
\(S{M^2} = S{H^2} + M{H^2}\) (định lí Pytago)
Xét tam giác SHM’ vuông tại H có
\(S{M’^2} = S{H^2} + M'{H^2}\) (định lí Pytago)
Mà SM = SM’ nên MH = MH’
+) Giả sử HM = HM’
Xét tam giác SHM vuông tại H có
\(S{M^2} = S{H^2} + M{H^2}\) (định lí Pytago)
Xét tam giác SHM’ vuông tại H có
\(S{M’^2} = S{H^2} + M'{H^2}\) (định lí Pytago)
Mà HM = HM’ nên SM = SM’
b) \(\begin{array}{l}MH > M’H \Leftrightarrow M{H^2} > M'{H^2}\\ \Leftrightarrow M{H^2} + S{H^2} > M'{H^2} + S{H^2} \Leftrightarrow S{M^2} > S{{M’}^2} \Leftrightarrow SM > SM’\end{array}\)