Nếu đường vuông góc chung \(\Delta \) cắt a, b tương ứng tại M. Trả lời Bài 34 trang 109 SGK Toán 11 tập 2 – Kết nối tri thức – Bài tập cuối năm. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và (widehat {BAD} = {60^0})….
Đề bài/câu hỏi:
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và \(\widehat {BAD} = {60^0}\). Biết \(SA \bot (ABCD)\) và \(SA = a\).
a) Chứng minh rằng \(BD \bot SC\).
b) Tính theo a khoảng cách giữa hai đường thẳng BD và SC.
Hướng dẫn:
Nếu đường vuông góc chung \(\Delta \) cắt a, b tương ứng tại M, N thì độ dài đoạn thẳng MN được gọi là khoảng cách giữa hai đường thẳng chéo nhau a, b.
Lời giải:
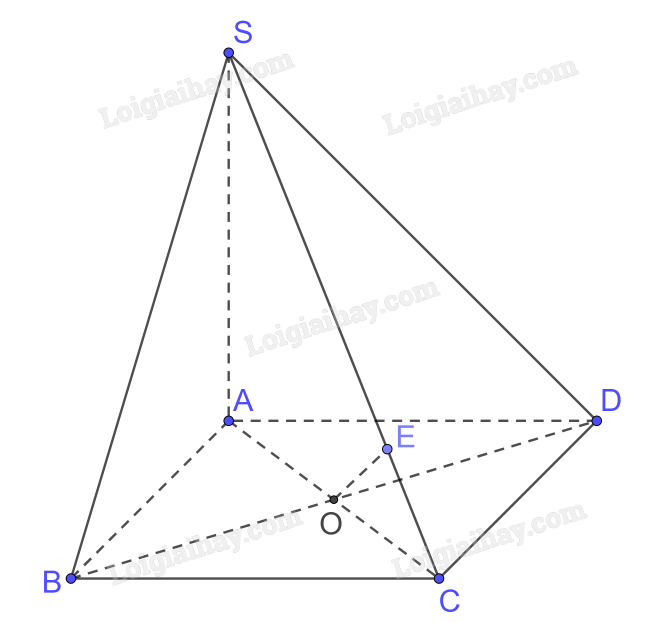
a) Ta có \(BD \bot AC,BD \bot SA \Rightarrow BD \bot \left( {SAC} \right);SC \subset \left( {SAC} \right) \Rightarrow BD \bot SC\)
b) Trong (SAC) kẻ \(OE \bot SC\)
Mà \(BD \bot \left( {SAC} \right) \Rightarrow OE \bot BD\)
\( \Rightarrow d\left( {BD,SC} \right) = OE\)
Gọi \(AC \cap BD = \left\{ O \right\}\)
Xét tam giác BAD có AB = AD, \(\widehat {BAD} = {60^0}\) \( \Rightarrow \) Tam giác BAD đều
\( \Rightarrow AO = \frac{{a\sqrt 3 }}{2} \Rightarrow AC = a\sqrt 3 \)
Xét tam giác SAC vuông tại A có
\(SC = \sqrt {S{A^2} + A{C^2}} = \sqrt {{a^2} + {{\left( {a\sqrt 3 } \right)}^2}} = 2a\)
Dễ dàng chứng minh được
\( \Rightarrow \frac{a}{{OE}} = \frac{{2a}}{{\frac{{a\sqrt 3 }}{2}}} \Rightarrow OE = \frac{{a\sqrt 3 }}{4}\)
Vậy \(d\left( {BD,SC} \right) = \frac{{a\sqrt 3 }}{4}\)