Bài 1.3 trang 16 Toán 11 tập 1 – Kết nối tri thức: Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau: a) 2π /3; b) – 11π /4; c) 150^0

Đề bài/câu hỏi:

Trên đường tròn lượng giác, xác định điểm M biểu diễn các góc lượng giác có số đo sau:

a) \(\frac{{2\pi }}{3}\); b) \( – \frac{{11\pi }}{4}\); c) \({150^0}\); d) \( – {225^0}\).

Hướng dẫn:

Để biểu diễn các góc lượng giác trên đường tròn lượng giác ta thường sử dụng các kết quả sau

– Góc \(\alpha \) và góc \(\alpha + k2\pi ,k\; \in \;\mathbb{Z}\) có cùng điểm biểu diễn trên đường tròn lượng giác.

– Số điểm trên đường tròn lượng giác biểu diễn bởi số đo có dạng \(\alpha + \frac{{k2\pi }}{m}\) (với k là số nguyên và m là số nguyên dương). Từ đó để biểu diễn các góc lượng giác đó ta lần lượt cho k từ 0 tới (m – 1) rồi biểu diễn các góc đó.

Lời giải:

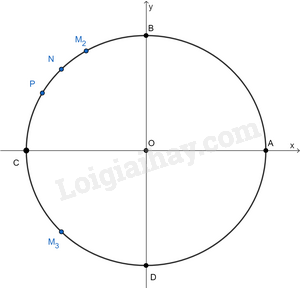
a) Ta có: \(\frac{{\frac{{2\pi }}{3}}}{{2\pi }} = \frac{1}{3}\). Ta chia đường tròn thành 3 phần bằng nhau. Khi đó điểm \({M_2}\) là điểm biểu diễn bởi góc có số đo \(\frac{{2\pi }}{3}\).

b) Ta có \( – \frac{{11\pi }}{4} = – \frac{{3\pi }}{4} + \left( { – 1} \right).2\pi \). Do đó điểm biểu diễn bởi góc \( – \frac{{11\pi }}{4}\) trùng với góc \( – \frac{{3\pi }}{4}\) và là điểm \({M_3}\).

c) Ta có \(\frac{{150}}{{180}} = \frac{5}{6}\). Ta chia nửa đường tròn thành 6 phần bằng nhau. Khi đó P là điểm biểu diễn bởi góc \({150^0}\)

d) Ta có \( – {225^0} = – {180^0} – {45^0}\). Do đó điểm biểu diễn N là điểm biểu diễn bởi góc \( – {225^0}\)