Đáp án Vận dụng 2 Bài 5. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện (trang 84, 85) – SGK Toán 11 Chân trời sáng tạo. Gợi ý: Cách xác định góc nhị diện \(\left[ {{P_1}, d, {Q_1}} \right]\.
Câu hỏi/Đề bài:
Cho biết kim tự tháp Memphis tại bang Tennessee (Mỹ) có dạng hình chóp tứ giác đều với chiều cao 98 m và cạnh đáy 180 m. Tính số đo góc nhị diện tạo bởi mặt bên và mặt đáy.
(Nguồn: https://en.wikipedia.org/wiki/Memphis Pyramid)

Hướng dẫn:
Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)
Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).
Bước 2: Tìm mặt phẳng \(\left( R \right) \supset c\).
Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).
Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).
Lời giải:
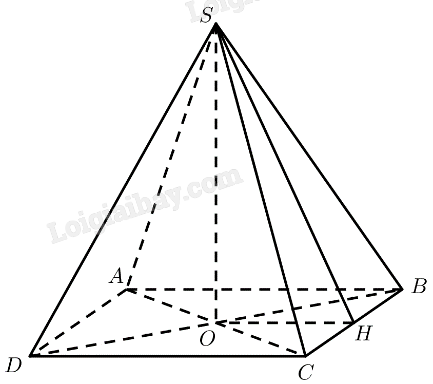
Mô hình hoá kim tự tháp bằng chóp tứ giác đều \(S.ABCD\) với \(O\) là tâm của đáy. Vậy \(AB = 180,SO = 98\)
Gọi \(H\) là trung điểm của \(BC\).
\(\Delta SBC\) đều \( \Rightarrow SH \bot BC\)
\(\Delta OBC\) vuông cân tại \(O \Rightarrow OH \bot BC\)
Vậy \(\widehat {SHO}\) là góc nhị diện tạo bởi mặt bên và mặt đáy.
Ta có: \(O\) là trung điểm của \(BD\)
\(H\) là trung điểm của \(BC\)
\( \Rightarrow OH\) là đường trung bình của \(\Delta BC{\rm{D}}\)
\( \Rightarrow OH = \frac{1}{2}CD = 90\)
\(\tan \widehat {SHO} = \frac{{SO}}{{OH}} = \frac{{49}}{{45}} \Rightarrow \widehat {SHO} \approx 47,{4^ \circ }\)
Vậy số đo góc nhị diện tạo bởi mặt bên và mặt đáy là \(47,{4^ \circ }\).