Trả lời Thực hành 3 Bài 4. Hàm số lượng giác và đồ thị (trang 28, 29, 30, 31, 32) – SGK Toán 11 Chân trời sáng tạo. Tham khảo: Dựa vào đồ thị hàm côsin để giải quyết.
Câu hỏi/Đề bài:
Li độ s (cm) của một con lắc đồng hộ theo thời gian t (giây) được cho bởi hàm số \(s = 2\cos \pi t\). Dựa vào đồ thị của hàm số côsin, hãy xác định ở các thời điểm t nào trong 1 giây đầu thì li độ s nằm trong đoạn \(\left[ { – 1;1} \right]\,\,(cm)\).

Hướng dẫn:
Dựa vào đồ thị hàm côsin để giải quyết
Lời giải:
Ta có: \(s \in \left[ { – 1;1} \right]\, \Leftrightarrow – 1 \le 2\cos \pi t \le 1\)
\( \Leftrightarrow – \frac{1}{2} \le \cos \pi t \le \frac{1}{2}\)
Trong 1 giây đầu tiên \(0 < t < 1\) \( \Rightarrow 0 < \pi t < \pi \).
Đồ thị hàm số \(y = cosx\) trên \(\left[ {0;\pi } \right]\):
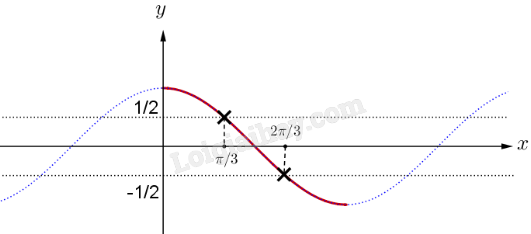
Dựa vào đồ thị ta thấy \( – \frac{1}{2} \le \cos \pi t \le \frac{1}{2} \Leftrightarrow \frac{\pi }{3} \le \pi t \le \frac{{2\pi }}{3} \Leftrightarrow \frac{1}{3} \le t \le \frac{2}{3}\)
Vậy \(t \in \left[ {\frac{1}{3};\frac{2}{3}} \right]\,\).