Trả lời Thực hành 3 Bài 2. Hai đường thẳng song song (trang 102, 103, 104, 105) – SGK Toán 11 Chân trời sáng tạo. Hướng dẫn: Sử dụng định lí 2: Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì.
Câu hỏi/Đề bài:
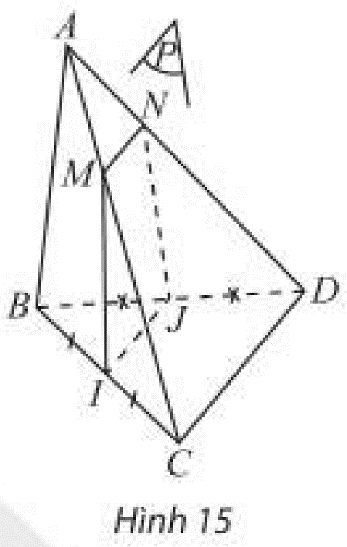
Cho tứ diện \(ABCD\) có \(I\) và \(J\) lần lượt là trung điểm của các cạnh \(BC\) và \(B{\rm{D}}\). Gọi \(\left( P \right)\) là mặt phẳng đi qua \(I,J\) và cắt hai cạnh \(AC\) và \(A{\rm{D}}\) lần lượt tại \(M\) và \(N\).
a) Chứng minh \(IJNM\) là một hình thang.
b) Tìm vị trí của điểm \(M\) dễ \(IJNM\) là hình bình hành.
Hướng dẫn:
Sử dụng định lí 2: Nếu ba mặt phẳng đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc đổi một song song.
Lời giải:
a) Ta có: \(I\) là trung điểm của \(BC\)
\(J\) là trung điểm của \(B{\rm{D}}\)
\( \Rightarrow IJ\) là đường trung bình của tam giác \(BCD\)
\( \Rightarrow IJ\parallel CD,IJ = \frac{1}{2}C{\rm{D}}\)
Ta có:
\(\begin{array}{l}IJ = \left( {BC{\rm{D}}} \right) \cap \left( P \right)\\MN = \left( {AC{\rm{D}}} \right) \cap \left( P \right)\\C{\rm{D}} = \left( {AC{\rm{D}}} \right) \cap \left( {BC{\rm{D}}} \right)\\IJ\parallel C{\rm{D}}\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(IJ\parallel MN\parallel C{\rm{D}}\).
Vậy \(IJNM\) là hình thang.
b) Để \(IJNM\) là hình bình hành thì \(IJ = MN\).
Mà \(IJ = \frac{1}{2}CD\) nên \(MN = \frac{1}{2}CD\).
Khi đó \(MN\) là đường trung bình của tam giác \(ACD\).
\( \Rightarrow M\) trung điểm của AC.