Giải chi tiết Thực hành 1 Bài 2. Hai đường thẳng song song (trang 100, 101, 102) – SGK Toán 11 Chân trời sáng tạo. Hướng dẫn: Dựa vào vị trí tương đối của hai đường thẳng trong không gian.
Câu hỏi/Đề bài:
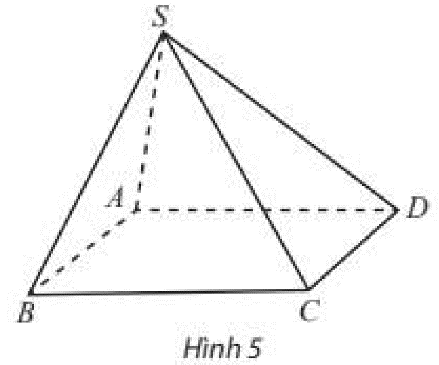
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Xét vị trí tương đối của các cặp đường thẳng sau đây:
a) \(AB\) và \(CD\);
b) \(SA\) và \(SC\);
c) \(SA\) và \(BC\).
Hướng dẫn:
Dựa vào vị trí tương đối của hai đường thẳng trong không gian:
• Trường hợp 1: Có một mặt phẳng chứa \(a\) và \(b\). Khi đó ta nói \(a\) và \(b\) đồng phẳng. Theo kết quả của hình học phẳng, có ba khả năng sau đây xảy ra:
‒ Nếu \(a\) và \(b\) có hai điểm chung thì ta nói \(a\) trùng \(b\).
‒ Nếu \(a\) và \(b\) có một điểm chung duy nhất M thì ta nói \(a\) và \(b\) cắt nhau tại M.
‒ Nếu \(a\) và \(b\) không có điểm chung thì ta nói \(a\) và \(b\) song song với nhau.
• Trường hợp 2: Không có mặt phẳng nào chứa cả \(a\) và \(b\). Khi đó ta nói hai đường thẳng \(a\) và \(b\) chéo nhau hay \(a\) chéo với \(b\).
Lời giải:
a) \(AB\) và \(CD\) cùng nằm trong mặt phẳng \(\left( {ABCD} \right)\).
\(ABCD\) là hình bình hành nên \(AB\parallel C{\rm{D}}\).
b) \(SA\) và \(SC\) cùng nằm trong mặt phẳng \(\left( {SAC} \right)\).
Do đó \(SA\) và \(SC\) cắt nhau tại \(S\).
c) Giả sử \(SA\) và \(BC\) cùng nằm trong mặt phẳng \(\left( P \right)\).
Suy ra đường thẳng \(AC\) cũng nằm trong \(\left( P \right)\).
Do đó \(\left( P \right)\) chứa cả 4 điểm của tứ diện \(SABC\) (vô lí do \(S\) không nằm trong mặt phẳng \(\left( {ABCD} \right)\)).
Vậy \(SA\) và \(BC\) không cùng nằm trong một mặt phẳng. Vậy \(SA\) và \(BC\) chéo nhau.