Trả lời Thực hành 1 Bài 1. Hai đường thẳng vuông góc (trang 54, 55) – SGK Toán 11 Chân trời sáng tạo. Gợi ý: Cách xác định góc giữa hai đường thẳng \(a\) và \(b\).
Câu hỏi/Đề bài:
Cho hình hộp \(ABCD.A’B’C’D’\) có 6 mặt đều là hình vuông \(M,N,E,F\) lần lượt là trung điểm các cạnh \(BC,BA,AA’,A’D’\). Tính góc giữa các cặp đường thẳng:
a) \(MN\) và \(DD’\);
b) \(MN\) và \(CD’\);
c) \(EF\) và \(CC’\).
Hướng dẫn:
Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):
Bước 1: Lấy một điểm \(O\) bất kì.
Bước 2: Qua điểm \(O\) dựng đường thẳng \(a’\parallel a\) và đường thẳng \(b’\parallel b\).
Bước 3: Tính \(\left( {a,b} \right) = \left( {a’,b’} \right)\).
Lời giải:
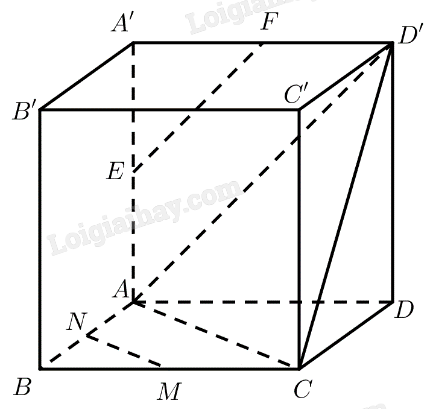
a) Ta có: \(M\) là trung điểm của \(BC\)
\(N\) là trung điểm của \(AB\)
\( \Rightarrow MN\) là đường trung bình của tam giác \(ABC\)
\( \Rightarrow MN\parallel AC\)
Mà \(DD’\parallel AA’\)
\( \Rightarrow \left( {MN,DD’} \right) = \left( {AC,AA’} \right) = \widehat {A’AC} = {90^ \circ }\).
b) Ta có: \(MN\parallel AC\)
\( \Rightarrow \left( {MN,CD’} \right) = \left( {AC,C{\rm{D}}’} \right) = \widehat {AC{\rm{D}}’}\)
Vì \(ABC{\rm{D}},ADD’A’,C{\rm{DD}}'{\rm{C}}’\) là các hình vuông bằng nhau nên các đường chéo của chúng bằng nhau. Vậy \(AC = A{\rm{D}}’ = C{\rm{D}}’\)
\( \Rightarrow \Delta AC{\rm{D}}’\) là tam giác đều \( \Rightarrow \widehat {AC{\rm{D}}’} = {60^ \circ }\).
Vậy \(\left( {MN,CD’} \right) = {60^ \circ }\).