Lời giải Hoạt động 3 Bài 3. Đường thẳng và mặt phẳng song song (trang 109, 110) – SGK Toán 11 Chân trời sáng tạo. Hướng dẫn: Để xác định vị trí tương đối của hai đường thẳng.
Câu hỏi/Đề bài:
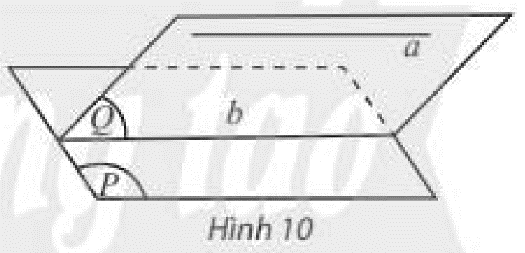
Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\) chứa \(a\) và cắt \(\left( P \right)\) theo giao tuyến \(b\) (Hình 10). Trong \(\left( Q \right)\), hai đường thẳng \(a,b\) có bao nhiều điểm chung?
Hướng dẫn:
Để xác định vị trí tương đối của hai đường thẳng, ta dựa vào số điểm chung của hai đường thẳng đó.
Lời giải:
Ta có: \(a\parallel \left( P \right) \Rightarrow \) Đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) không có điểm chung.
\(\left( P \right) \cap \left( Q \right) = b \Rightarrow b \subset \left( P \right)\)
Do đó hai đường thẳng \(a,b\) không có điểm chung.