Lời giải Hoạt động 1 Bài 5. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện (trang 82, 83) – SGK Toán 11 Chân trời sáng tạo. Hướng dẫn: Sử dụng tính chất: Đường thẳng vuông góc với mặt phẳng thì nó vuông góc với mọi đường thẳng nằm.
Câu hỏi/Đề bài:
Cho đường thẳng \(a\) và mặt phẳng \(\left( P \right)\).
a) Trong trường hợp \(a\) vuông góc với \(\left( P \right)\), tìm góc giữa \(a\) và một đường thẳng \(b\) tuỳ ý trong \(\left( P \right)\).
b) Trong trường hợp \(a\) không vuông góc với \(\left( P \right)\), tìm góc giữa \(a\) và đường thẳng \(a’\) là hình chiếu vuông góc của \(a\) trên \(\left( P \right)\).
Hướng dẫn:
Sử dụng tính chất: Đường thẳng vuông góc với mặt phẳng thì nó vuông góc với mọi đường thẳng nằm trong mặt phẳng.
Lời giải:
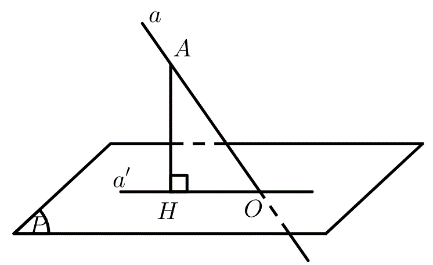
a) Ta có:
\(\left. \begin{array}{l}a \bot \left( P \right)\\b \subset \left( P \right)\end{array} \right\} \Rightarrow a \bot b \Rightarrow \left( {a,b} \right) = {90^ \circ }\)
b) Lấy \(A \in a\). Gọi \(O = a \cap \left( P \right)\). Dựng \(AH \bot a’\left( {H \in a’} \right)\).
Ta có: \(\left( {a,a’} \right) = \left( {AO,OH} \right) = \widehat {AOH}\)