Hướng dẫn giải Hoạt động 1 Bài 3. Các công thức lượng giác (trang 21) – SGK Toán 11 Chân trời sáng tạo. Gợi ý: Dựa vào hình vẽ và 2 công thức tính tích vô hướng để giải quyết.
Câu hỏi/Đề bài:
Quan sát Hình 1. Từ hai cách tính tích vô hướng của vectơ \(\overrightarrow {OM} ,\overrightarrow {ON} \) sau đây:
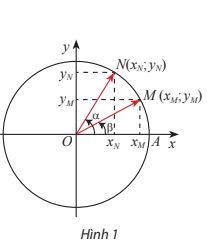
\(\overrightarrow {OM} .\overrightarrow {ON} = \left| {\overrightarrow {OM} } \right|.\left| {\overrightarrow {ON} } \right|.cos\left( {\overrightarrow {OM} ,\overrightarrow {ON} } \right)\)\( = cos\left( {\overrightarrow {OM} ,\overrightarrow {ON} } \right) = cos\left( {\alpha – \beta } \right)\)
\(\overrightarrow {OM} .\overrightarrow {ON} = {x_M}.{x_N} + {y_M}.{y_N}\)
Hãy suy ra công thức tính cos(α – β) theo các giá trị lượng giác của α và β. Từ đó, hãy suy ra công thức cos(α + β) bằng cách thay β bằng – β.
Hướng dẫn:
Dựa vào hình vẽ và 2 công thức tính tích vô hướng để giải quyết
Lời giải:
Ta có:
\(cos\left( {\alpha – \beta } \right) = {x_M}.{x_N} + {y_M}.{y_N} = cos\alpha .cos\beta + \sin \alpha .\sin \beta \)
\(cos\left( {\alpha + \beta } \right) = cos\left( {\alpha – \left( { – \beta } \right)} \right) = cos\alpha .cos\left( { – \beta } \right) + \sin \alpha .\sin \left( { – \beta } \right) = cos\alpha .cos\beta – \sin \alpha .\sin \beta \)