Bài 6 trang 56 Toán 11 tập 2 – Chân trời sáng tạo: Một ô che nắng có viền khung hình lục giác đều ABCDEF song song với mặt bàn và có cạnh AB song song với cạnh bàn a (Hình 5)

Đề bài/câu hỏi:

Một ô che nắng có viền khung hình lục giác đều \(ABCDEF\) song song với mặt bàn và có cạnh \(AB\) song song với cạnh bàn \(a\) (Hình 5). Tinh số đo góc hợp bởi đường thẳng \(a\) lần lượt với các đường thẳng \(AF,AE\) và \(A{\rm{D}}\).

Hướng dẫn:

Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):

Bước 1: Lấy một điểm \(O\) bất kì.

Bước 2: Qua điểm \(O\) dựng đường thẳng \(a’\parallel a\) và đường thẳng \(b’\parallel b\).

Bước 3: Tính \(\left( {a,b} \right) = \left( {a’,b’} \right)\).

Lời giải:

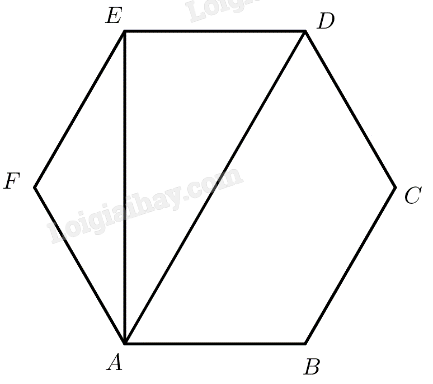
Ta có: \(AB\parallel a \Rightarrow \left( {AF,a} \right) = \left( {AF,AB} \right)\)

\(ABCDEF\) là lục giác đều \( \Rightarrow \widehat {F{\rm{A}}B} = {120^ \circ } \Rightarrow \left( {AB,a} \right) = {180^ \circ } – \widehat {F{\rm{A}}B} = {60^ \circ }\)

\(ABCDEF\) là lục giác đều

\(\begin{array}{l} \Rightarrow \widehat {AFE} = {120^ \circ } \Rightarrow \widehat {F{\rm{AE}}} = \frac{{{{180}^ \circ } – \widehat {AFE}}}{2} = {30^ \circ }\\ \Rightarrow \widehat {E{\rm{A}}B} = \widehat {F{\rm{A}}B} – \widehat {F{\rm{AE}}} = {90^ \circ }\end{array}\)

\(AB\parallel a \Rightarrow \left( {AE,a} \right) = \left( {AE,AB} \right) = \widehat {E{\rm{A}}B} = {90^ \circ }\)

\(ABC{\rm{D}}\) là hình thang cân \( \Rightarrow \widehat {BA{\rm{D}}} = {60^ \circ }\)

\(AB\parallel a \Rightarrow \left( {AD,a} \right) = \left( {AD,AB} \right) = \widehat {D{\rm{A}}B} = {60^ \circ }\)