Dựa vào hình vẽ và sử dụng đồ thị hàm số sin để trả lời. Gợi ý giải Bài 6 trang 33 SGK Toán 11 tập 1 – Chân trời sáng tạo – Bài 4. Hàm số lượng giác và đồ thị. Khoảng cách từ tâm một guồng nước đến mặt nước và bán kính của guồng đều bằng 3m….
Đề bài/câu hỏi:
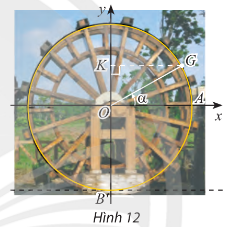
Khoảng cách từ tâm một guồng nước đến mặt nước và bán kính của guồng đều bằng 3m. Xét gàu G của guồng. Ban đầu gàu G nằm ở vị trí A (Hình 12)
a) Viết hàm số h biểu diễn chiều cao (tính bằng mét) của gàu G so với mặt nước theo góc \(\alpha = (OA,OG)\)
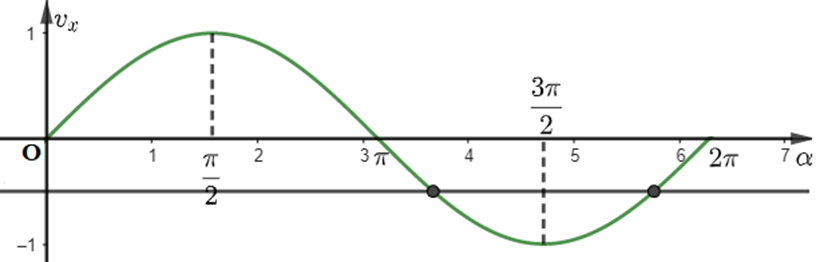
b) Guồng nước quay hết mỗi vòng trong 30 giây. Dựa vào đồ thị của hàm số sin, hãy cho biết ở các thời điểm t nào trong 1 phút đầu, khoảng cách của gàu đến mặt nước bằng 1,5m.
Hướng dẫn:
Dựa vào hình vẽ và sử dụng đồ thị hàm số sin để trả lời.
Lời giải:
a) Điểm G là điểm biểu diễn cho góc lượng giác có số đo \(\alpha \). Khi đó tọa độ điểm \(G\left( {3cos\alpha ;{\rm{ }}3sin\alpha } \right)\).
Chiều cao của gàu ở vị trí G đến mặt nước là: \(3{\rm{ }} + {\rm{ }}3sin\alpha \) (m).
b) b) Khoảng cách của gàu đến mặt nước bằng 1,5m khi \(3 + 3sin\alpha = 1,5 \Leftrightarrow sin\alpha {\rm{ }} = \frac{{ – 1}}{2}\)
Một vòng quay là 30 giây và t nằm trong khoảng từ 0 đến 1 phút do đó t ∈ [0; 2π].