‒ Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng. Trả lời Bài 4 trang 85 SGK Toán 11 tập 2 – Chân trời sáng tạo – Bài 5. Góc giữa đường thẳng và mặt phẳng. Góc nhị diện. Một con dốc có dạng hình lăng trụ đứng tam giác với kích thước như trong Hình 9….
Đề bài/câu hỏi:
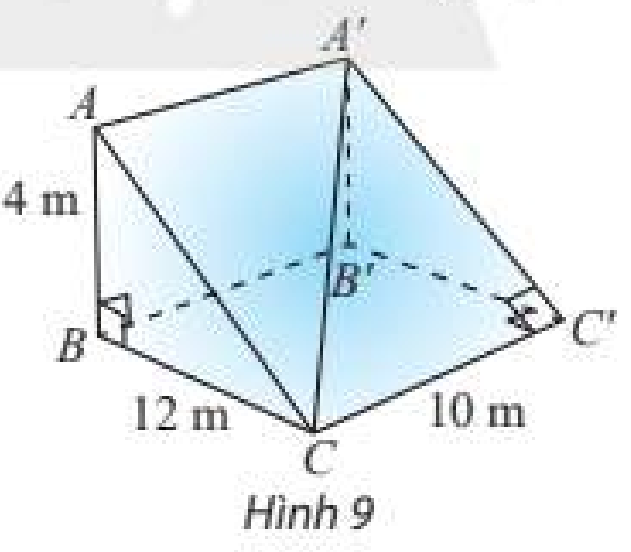
Một con dốc có dạng hình lăng trụ đứng tam giác với kích thước như trong Hình 9.
a) Tính số đo góc giữa đường thẳng \(CA’\) và .
b) Tính số đo góc nhị diện cạnh \(CC’\).
Hướng dẫn:
‒ Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.
‒ Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)
Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).
Bước 2: Tìm mặt phẳng \(\left( R \right) \supset c\).
Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).
Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).
Lời giải:
a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}BB’ \bot \left( {A’B’C’} \right) \Rightarrow BB’ \bot A’B’\\A’B’ \bot B’C’\end{array} \right\} \Rightarrow A’B’ \bot \left( {CC’B’B} \right)\\ \Rightarrow \left( {CA’,\left( {CC’B’B} \right)} \right) = \left( {CA’,CB’} \right) = \widehat {A’CB’}\\B’C = \sqrt {BB{‘^2} + B{C^2}} = 2\sqrt {61} ,A’B’ = AB = 4\\\tan \widehat {A’CB’} = \frac{{A’B’}}{{B’C}} = \frac{2}{{\sqrt {61} }} \Rightarrow \widehat {A’CB’} \approx 14,{4^ \circ }\end{array}\)
Vậy \(\left( {CA’,\left( {CC’B’B} \right)} \right) \approx 14,{4^ \circ }\)
b) \(CC’ \bot \left( {ABC} \right) \Rightarrow CC’ \bot AC,CC’ \bot BC\)
Vậy \(\widehat {ACB}\) là góc nhị diện cạnh \(CC’\).
\(\tan \widehat {ACB} = \frac{{AB}}{{AC}} = \frac{1}{3} \Rightarrow \widehat {ACB} \approx 18,{4^ \circ }\)