Cách xác định góc giữa hai đường thẳng \(a\) và \(b\): Bước 1: Lấy một điểm \(O\) bất kì. Bước 2: Qua điểm \(O\. Phân tích, đưa ra lời giải Bài 4 trang 56 SGK Toán 11 tập 2 – Chân trời sáng tạo – Bài 1. Hai đường thẳng vuông góc. Cho tứ diện đều (ABCD) cạnh (a). Gọi (K) là trung điểm của (CD)….
Đề bài/câu hỏi:
Cho tứ diện đều \(ABCD\) cạnh \(a\). Gọi \(K\) là trung điểm của \(CD\). Tính góc giữa hai đường thẳng \(AK\) và \(BC\).
Hướng dẫn:
Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):
Bước 1: Lấy một điểm \(O\) bất kì.
Bước 2: Qua điểm \(O\) dựng đường thẳng \(a’\parallel a\) và đường thẳng \(b’\parallel b\).
Bước 3: Tính \(\left( {a,b} \right) = \left( {a’,b’} \right)\).
Lời giải:
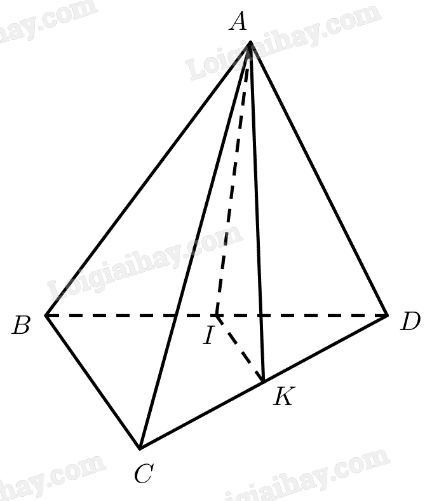
Gọi \(I\) là trung điểm của \(B{\rm{D}}\).
Ta có: \(I\) là trung điểm của \(B{\rm{D}}\)
\(K\) là trung điểm của \(CD\)
\( \Rightarrow IK\) là đường trung bình của tam giác \(BCD\)
\( \Rightarrow IK\parallel BC \Rightarrow \left( {AK,BC} \right) = \left( {AK,IK} \right) = \widehat {AKI}\)
\(IK = \frac{1}{2}BC = \frac{a}{2}\)
\(AI\) là trung tuyến của tam giác \(AB{\rm{D}}\)\( \Rightarrow AI = \frac{{\sqrt {2\left( {A{B^2} + A{{\rm{D}}^2}} \right) – B{{\rm{D}}^2}} }}{2} = \frac{{a\sqrt 3 }}{2}\)
\(AK\) là trung tuyến của tam giác \(AC{\rm{D}}\)\( \Rightarrow AK = \frac{{\sqrt {2\left( {A{C^2} + A{{\rm{D}}^2}} \right) – C{{\rm{D}}^2}} }}{2} = \frac{{a\sqrt 3 }}{2}\)
Xét tam giác \(AIK\) có:
\(\cos \widehat {AKI} = \frac{{A{K^2} + I{K^2} – A{I^2}}}{{2.AK.IK}} = \frac{{\sqrt 3 }}{6} \Rightarrow \widehat {AKI} \approx {73^ \circ }13’\)
Vậy \(\left( {AK,BC} \right) \approx {73^ \circ }13’\).