Cách chứng minh hai mặt phẳng vuông góc: chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng. Giải chi tiết Bài 3 trang 86 SGK Toán 11 tập 2 – Chân trời sáng tạo – Bài tập cuối Chương 8. Cho hình chóp (S.ABCD) có các cạnh bên và cạnh đáy đều bằng (a)….
Đề bài/câu hỏi:
Cho hình chóp \(S.ABCD\) có các cạnh bên và cạnh đáy đều bằng \(a\). Gọi \(M\) là trung điểm của \({\rm{S}}A\). Mặt phẳng \(\left( {MBD} \right)\) vuông góc với mặt phẳng nào dưới đây?
A. \(\left( {SBC} \right)\).
C. \(\left( {SBD} \right)\).
B. \(\left( {SAC} \right)\).
D. \(\left( {ABCD} \right)\).
Hướng dẫn:
Cách chứng minh hai mặt phẳng vuông góc: chứng minh mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng.
Lời giải:
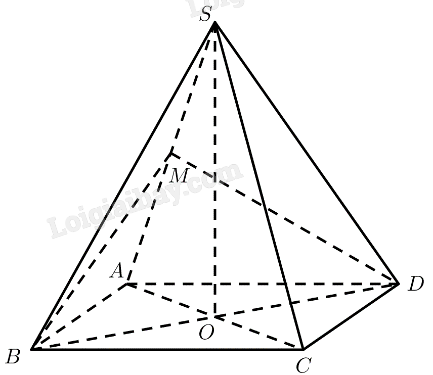
Gọi \(O\) là tâm của đáy \( \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow SO \bot B{\rm{D}}\)
\(ABC{\rm{D}}\) là hình vuông \( \Rightarrow AC \bot B{\rm{D}}\)
\(\left. \begin{array}{l} \Rightarrow B{\rm{D}} \bot \left( {SAC} \right)\\B{\rm{D}} \subset \left( {MB{\rm{D}}} \right)\end{array} \right\} \Rightarrow \left( {MB{\rm{D}}} \right) \bot \left( {SAC} \right)\)
Chọn B.