‒ Sử dụng công thức tính thể tích lăng trụ: \(V = Sh\). Phân tích, đưa ra lời giải Bài 13 trang 87 SGK Toán 11 tập 2 – Chân trời sáng tạo – Bài tập cuối Chương 8. Cho hình hộp \(ABCD.A’B’C’D’\) có cạnh bên \(AA’ = a\), đáy \(ABCD\…
Đề bài/câu hỏi:
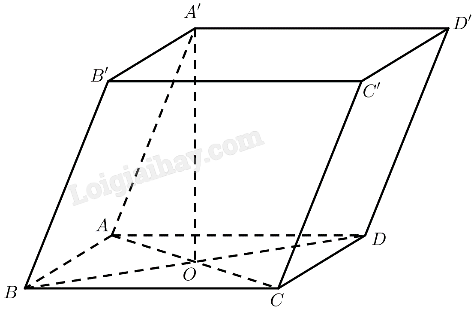
Cho hình hộp \(ABCD.A’B’C’D’\) có cạnh bên \(AA’ = a\), đáy \(ABCD\) là hình thoi có \(AB = BD = a\). Hình chiếu vuông góc của \(A’\) lên mặt đáy trùng với điểm \(O\) là giao điểm hai đường chéo của đáy. Tính thể tích của khối hộp.
Hướng dẫn:
‒ Sử dụng công thức tính thể tích lăng trụ: \(V = Sh\).
Lời giải:
\(AB = B{\rm{D}} = A{\rm{D}} = a \Rightarrow \Delta ABD\) đều\( \Rightarrow \widehat {BA{\rm{D}}} = {60^ \circ }\)
\(O\) là trung điểm của \(BD\)\( \Rightarrow AO = \frac{{AB\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{2}\)
\(\begin{array}{l}AA’ \bot \left( {ABCD} \right) \Rightarrow AA’ \bot AO\\ \Rightarrow A’O = \sqrt {AA{‘^2} – A{O^2}} = \frac{a}{2}\end{array}\)
\({S_{ABC{\rm{D}}}} = AB.A{\rm{D}}.\sin \widehat {BA{\rm{D}}} = \frac{{{a^2}\sqrt 3 }}{2}\)
\({V_{ABCD.A’B’C’D’}} = {S_{ABC{\rm{D}}}}.A’O = \frac{{{a^3}\sqrt 3 }}{4}\)