Đáp án Luyện tập 3 Bài 2. Hai đường thẳng song song trong không gian (trang 97, 98, 99, 100) – SGK Toán 11 Cánh diều. Hướng dẫn: Nếu ba mp phân biệt đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến.
Câu hỏi/Đề bài:
Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của các đoạn thẳng SA, SC. Lấy các điểm P, Q lần lượt thuộc các đoạn thẳng AB, BC sao cho \(\frac{{BP}}{{BA}} = \frac{{BQ}}{{BC}} = \frac{1}{3}\). Chứng minh rằng MN song song với PQ.
Hướng dẫn:
– Nếu ba mp phân biệt đôi một cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến ấy hoặc đồng quy hoặc song song với nhau
– Hệ quả: Nếu hai mp phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó
– Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì song song với nhau
\(\left\{ \begin{array}{l}a \ne b\\a//c\\b//c\end{array} \right. \Rightarrow a//b\)
Lời giải:
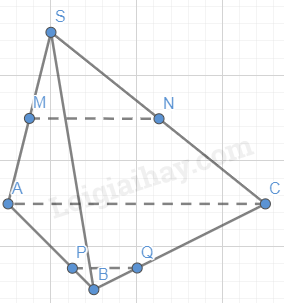
Ta có M, N lần lượt là trung điểm của SA, SC
Do đó, tam giác SAC có MN // AC (1)
Ta có: \(\frac{{BP}}{{BA}} = \frac{{BQ}}{{BC}} = \frac{1}{3}\)
Suy ra: PQ // AC (2)
Từ (1) và (2), suy ra: MN // PQ