Giải chi tiết Hoạt động 6 Bài 3. Hàm số mũ. Hàm số lôgarit (trang 43, 44) – SGK Toán 11 Cánh diều. Gợi ý: Áp dụng kiến thức đã học về giới hạn và lũy thừa để trả lời câu hỏi.
Câu hỏi/Đề bài:
Cho hàm số lôgarit \(y = {\log _{\frac{1}{2}}}x\)
a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau:

b, Trong mặt phẳng tọa độ Oxy, biểu diễn các điểm (x; y) trong bảng giá trị ở câu a.
Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;{{\log }_{\frac{1}{2}}}x} \right)\) với \(x \in (0; + \infty )\) và nối lại ta được đồ thị hàm số \(y = {\log _{\frac{1}{2}}}x\) như hình bên.
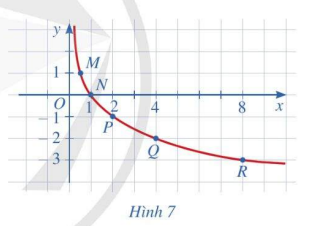
c, Cho biết tọa độ giao điểm của đồ thị hàm số \(y = {\log _{\frac{1}{2}}}x\) với trục hoành và vị trí của đồ thị hàm số đó với trục tung.
d, Quan sát đồ thị hàm số \(y = {\log _{\frac{1}{2}}}x\), nêu nhận xét về:
- \(\mathop {\lim }\limits_{x \to {0^ + }} ({\log _{\frac{1}{2}}}x)\,;\mathop {\,\,\mathop {\lim }\limits_{x \to + \infty } ({{\log }_{\frac{1}{2}}}x)}\limits_{} \)
- Sự biến thiên của hàm số \(y = {\log _{\frac{1}{2}}}x\) và lập bảng biến thiên của hàm số đó.
Hướng dẫn:
Áp dụng kiến thức đã học về giới hạn và lũy thừa để trả lời câu hỏi
Lời giải:
a) \(y = {\log _{\frac{1}{2}}}x\)

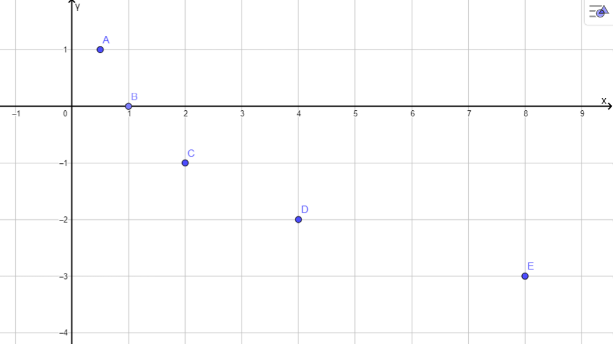
b, Biểu diễn các điểm ở câu a:
c, Tọa độ giao điểm của đồ thị hàm số với trục hoành \(y = {\log _{\frac{1}{2}}}x\)là (1;0)
Đồ thị hàm số đó không cắt trục tung
c) \(\mathop {\lim }\limits_{x \to {0^ + }} {\log _{\frac{1}{2}}}x = 0;\,\,\mathop {\lim }\limits_{x \to + \infty } {\log _{\frac{1}{2}}}x = – \infty \)
Hàm số \(y = {\log _{\frac{1}{2}}}x\) nghịch biến trên toàn \((0; + \infty )\)
Bảng biến thiên của hàm số:
