Giải Hoạt động 5 Bài 1. Các số đặc trưng xu thế trung tâm cho mẫu số liệu ghép nhóm (trang 8) – SGK Toán 11 Cánh diều. Hướng dẫn: Dựa vào công thức đã học và công thức được cho để trả lời câu hỏi.
Câu hỏi/Đề bài:
Trong phòng thí nghiệm, người ta chia 99 mẫu vật thành năm nhóm căn cứ trên khối lượng của chúng (đơn vị: gam) và lập bảng tần số ghép nhóm bao gồm cả tần số tích lũy như Bảng 10.
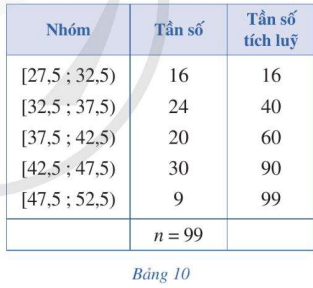
a) Nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng: \(\frac{n}{2} = \frac{{99}}{2} = 49,5\) có đúng không?
b) Tìm đầu mút trái \(r\), độ dài \(d\), tần số \({n_3}\) của nhóm 3; tần số tích lũy \(c{f_2}\) của nhóm 2.
c) Tính giá trị \({M_e}\) theo công thức sau: \({M_e} = r + \left( {\frac{{49,5 – c{f_2}}}{{{n_3}}}} \right).d\)
Hướng dẫn:
Dựa vào công thức đã học và công thức được cho để trả lời câu hỏi
Lời giải:
a) Nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 49,5
b) + Đầu mút trái của nhóm 3: 32,5
+ Độ dài của nhóm 3: 42,5 – 37,5 = 5
+ Tần số của nhóm 3: 20
+ Tần số tích lũy \(c{f_2}\) của nhóm 2: 40
c) \({M_e} = 32,5 + \left( {\frac{{49,5 – 40}}{{20}}} \right).5 = 34,875\)