Bài 5 trang 94 Toán 11 tập 2 – Cánh diều: Trong Hình 43, xét các góc nhị diện có góc phẳng nhị diện tương ứng là ∠ B, ∠ C, ∠ D, ∠ E trong cùng mặt phẳng. Lục giác ABCDEG

Đề bài/câu hỏi:

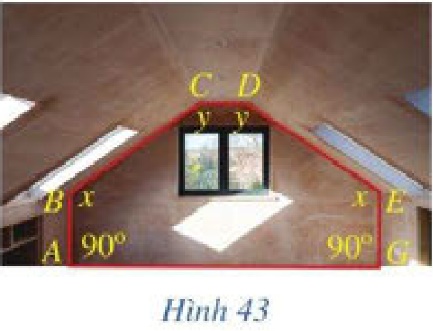
Trong Hình 43, xét các góc nhị diện có góc phẳng nhị diện tương ứng là \(\widehat B,\widehat C,\widehat D,\widehat E\) trong cùng mặt phẳng. Lục giác \(ABCDEG\) nằm trong mặt phẳng đó có \(AB = GE = 2{\rm{ }}m,BC = DE,\widehat A = \widehat G = {90^ \circ },\widehat B = \widehat E = x,\widehat C = \widehat D = y\). Biết rằng khoảng cách từ \(C\) và \({\rm{D}}\) đến \({\rm{AG}}\) là \(4{\rm{ }}m\), \(AG = 12{\rm{ }}m,CD = 1{\rm{ }}m\). Tìm x, y (làm tròn kết quả đến hàng đơn vị theo đơn vị độ).

Hướng dẫn:

Sử dụng công thức tính thể tích khối chóp cụt đều: \(V = \frac{1}{3}h\left( {S + \sqrt {SS’} + S’} \right)\).

Lời giải:

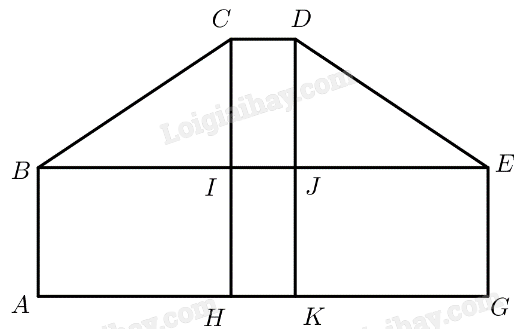
Kẻ \(CH \bot AG\left( {H \in AG} \right),DK \bot AG\left( {K \in AG} \right)\)

Gọi \(I = BE \cap CH,J = BE \cap DK\).

\(ABEG\) là hình chữ nhật \( \Rightarrow BE = AB = 12\)

\(C{\rm{D}}KH,C{\rm{D}}JI\) là hình chữ nhật \( \Rightarrow HK = IJ = C{\rm{D}} = 1\)

\(ABIH,EGKJ\) là hình chữ nhật \( \Rightarrow IH = JK = AB = 2\)

\(AH = GK = BI = EJ = \frac{{AG – HK}}{2} = \frac{{12 – 1}}{2} = 5,5\)

\(CH = d\left( {C,AG} \right) = 4 \Rightarrow CI = CH – IH = 4 – 2 = 2\)

\(\Delta BCI\) vuông tại \(I\)\( \Rightarrow \tan \widehat {CBI} = \frac{{CI}}{{BI}} = \frac{2}{{5,5}} = \frac{4}{{11}} \Rightarrow \widehat {CBI} \approx 19,{98^ \circ }\)

\(\begin{array}{l} \Rightarrow x = \widehat {ABI} + \widehat {CBI} = {90^ \circ } + 19,{98^ \circ } = 110,{0^ \circ }\\ \Rightarrow y = {180^ \circ } – x = {180^ \circ } – 110,{0^ \circ } = 70,{0^ \circ }\end{array}\)