Áp dụng định lý sau Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông. Gợi ý giải Giải bài 7.6 trang 28 sách bài tập toán 11 – Kết nối tri thức với cuộc sống – Bài 23. Đường thẳng vuông góc với mặt phẳng. Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\) và đáy là tam giác \(ABC\…
Đề bài/câu hỏi:
Cho hình chóp \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \(\left( {ABC} \right)\) và đáy là tam giác \(ABC\) vuông tại\(B\). Kẻ \(AM\) vuông góc với \(SB\) tại \(M\) và \(AN\) vuông góc với \(SC\) tại\(N\). Chứng minh rằng:
a)\(BC \bot \left( {SAB} \right)\);
b) \(AM \bot \left( {SBC} \right)\)
c) \(SC \bot \left( {AMN} \right)\)
Hướng dẫn:
Áp dụng định lý sau
Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng
một mặt phẳng thì nó vuông góc với mặt phẳng đó.
Chứng minh hai đường thẳng vuông góc dựa vào đường thẳng vuông góc với mặt phẳng
+ \(\left\{ \begin{array}{l}a \bot \left( \alpha \right)\\b \subset \alpha \end{array} \right. \Rightarrow a \bot b\)
Lời giải:
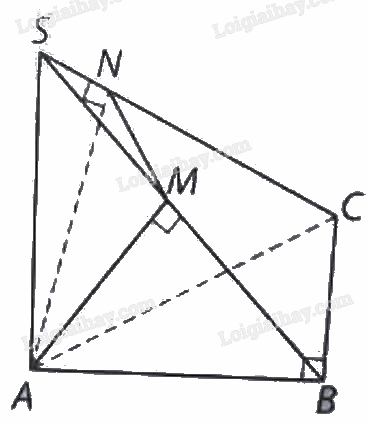
a) Ta có: \(BC \bot AB\)và \(SA \bot \left( {ABC} \right)\) nên\(SA \bot BC\), suy ra \(BC \bot \left( {SAB} \right).\)
b) Vì \(BC \bot \left( {SAB} \right).\) nên \(BC \bot AM.\), mà \(AM \bot SB.\), suy ra \(AM \bot \left( {SBC} \right).\)
c) Vì \(AM \bot \left( {SBC} \right).\) nên \(AM \bot SC.\), mà \(AN \bot SC.\), suy ra \(\left( {AMN} \right) \bot SC.\).