Gọi \(O\) là giao điểm của \(A’C’\) và \(B’D’\) Xác định hình chiếu vuông góc của \(AA’\) trên mặt phẳng \(\left( {A’B’CD’} \right)\. Hướng dẫn trả lời Giải bài 7.16 trang 31 sách bài tập toán 11 – Kết nối tri thức với cuộc sống – Bài 24. Phép chiếu vuông góc với mặt phẳng. Cho hình hộp \(ABCD \cdot A’B’C’D’\) có đáy \(ABCD\) là hình vuông cạnh a và \(AA’ = a\sqrt 2 \…
Đề bài/câu hỏi:
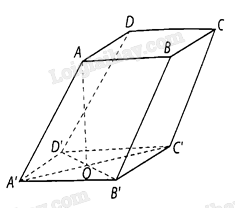
Cho hình hộp \(ABCD \cdot A’B’C’D’\) có đáy \(ABCD\) là hình vuông cạnh a và \(AA’ = a\sqrt 2 \), hình chiếu vuông góc của \(A\) trên mặt phẳng \(\left( {A’B’C’D’} \right)\) trùng với trung điểm của \(B’D’\). Tính góc giữa đường thẳng \(AA’\) và mặt phẳng \(\left( {A’B’C’D’} \right)\).
Hướng dẫn:
Gọi \(O\) là giao điểm của \(A’C’\) và \(B’D’\)
Xác định hình chiếu vuông góc của \(AA’\) trên mặt phẳng \(\left( {A’B’CD’} \right)\)
Tính góc giữa đường thẳng \(AA’\) và hình chiếu của nó rồi kết luận
Áp dụng tỉ số lượng giác cho tam giác vuông để tính góc
Lời giải:
Gọi \(O\) là giao điểm của \(A’C’\) và \(B’D’\).
Ta có: \(A’O\) là hình chiếu vuông góc của \(AA’\) trên mặt phẳng \(\left( {A’B’CD’} \right)\), góc giữa đường thẳng \(AA’\) và mặt phẳng \(\left( {A’B’C’D’} \right)\) bằng góc giữa \(AA’\) và \(A’O\).
Mà \(\left( {AA’,A’O} \right) = \widehat {AA’O}\), ta lại có \(A’O = \frac{{a\sqrt 2 }}{2}\).
Do đó \({\rm{cos}}\widehat {AA’O} = \frac{{OA’}}{{AA’}} = \frac{1}{2}\),
Suy ra \(\widehat {AA’O} = {60^ \circ }\).
Vậy góc giữa đường thẳng \(AA’\) và mặt phẳng \(\left( {A’B’C’D’} \right)\) bằng \({60^ \circ }\).