Giải chi tiết Câu 8 Bài tập cuối chương 5 (trang 160) – SBT Toán 11 Chân trời sáng tạo. Tham khảo: Sử dụng kiến thức xác định trung vị của mẫu số liệu ghép nhóm để tính.
Câu hỏi/Đề bài:
Trả lời các câu hỏi 6-10 dựa trên bảng số liệu về chiều cao của 100 học sinh một trường trung học phổ thông dưới đây.
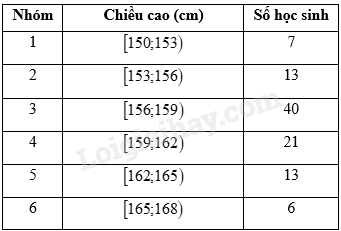
Trung vị của mẫu số liệu ghép nhóm trên là
A. 157,76.
B. 157,25.
C. 158,25.
D. 160,45.
Hướng dẫn:
Sử dụng kiến thức xác định trung vị của mẫu số liệu ghép nhóm để tính:
Gọi n là cỡ mẫu.
Giả sử nhóm \(\left[ {{u_m};{u_{m + 1}}} \right)\) chứa trung vị, \({n_m}\) là tần số của nhóm chứa trung vị,
\(C = {n_1} + {n_2} + … + {n_{m – 1}}\).
Khi đó, trung vị của mẫu số liệu là: \({M_e} = {u_m} + \frac{{\frac{n}{2} – C}}{{{n_m}}}.\left( {{u_{m + 1}} – {u_m}} \right)\).
Lời giải:
Gọi \({x_1},{x_2},…,{x_{100}}\) là mẫu số liệu được xếp theo thứ tự không giảm
Do cỡ mẫu \(n = 100\) nên trung vị của mẫu số liệu là \(\frac{{{x_{50}} + {x_{51}}}}{2}\). Do đó trung vị của mẫu số liệu thuộc nhóm \(\left[ {156;159} \right)\).
Trung vị của mẫu số liệu ghép nhóm là: \({M_e} = 156 + \frac{{\frac{{100}}{2} – \left( {7 + 13} \right)}}{{40}}.\left( {159 – 156} \right) = 158,25\)
Chọn C