Giải chi tiết Câu 11 Bài tập cuối chương 8 (trang 74, 75) – SBT Toán 11 Chân trời sáng tạo. Tham khảo: Sử dụng kiến thức về góc giữa hai mặt phẳng để tính.
Câu hỏi/Đề bài:
Cho hình chóp S.ABCD có đáy là hình chữ nhật, \(AB = 2a,AD = a\). Tam giác SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Góc giữa mặt phẳng (SBC) và (ABCD) bằng \({45^0}\). Khi đó thể tích khối chóp S.ABCD là
A. \(\frac{{\sqrt 3 }}{3}{a^3}\)
B. \(\frac{1}{3}{a^3}\)
C. \(2{a^3}\)
D. \(\frac{2}{3}{a^3}\)
Hướng dẫn:
+ Sử dụng kiến thức về góc giữa hai mặt phẳng để tính: Góc giữa hai mặt phẳng cắt nhau bằng góc giữa hai đường thẳng lần lượt nằm trong hai mặt phẳng và vuông góc với giao tuyến của hai mặt phẳng.
+ Sử dụng kiến thức về thể tích hình chóp: Thể tích hình chóp bằng một phần ba diện tích đáy nhân với chiều cao: \(V = \frac{1}{3}S.h\)
Lời giải:
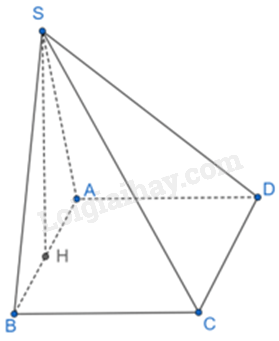
Gọi H là trung điểm của AB. Vì tam giác SAB cân tại S nên SH là đường trung tuyến đồng thời là đường cao. Do đó, \(SH \bot AB\)
Vì \(\left( {SAB} \right) \bot \left( {ABCD} \right),SH \bot AB,SH \subset \left( {SAB} \right)\), AB là giao tuyến của (SAB) và (ABCD). Do đó, \(SH \bot \left( {ABCD} \right) \Rightarrow SH \bot BC\)
Vì ABCD là hình chữ nhật nên \(BC \bot AB\)
Mà \(SH \bot BC\), SH và AB cắt nhau tại H và nằm trong mặt phẳng SAB nên \(BC \bot \left( {SAB} \right)\)
Lại có: \(SB \subset \left( {SAB} \right) \Rightarrow BC \bot SB\)
Ta có: \(BC \bot SB,AB \bot BC,SB \subset \left( {SBC} \right),AB \subset \left( {ABCD} \right)\), BC là giao tuyến của 2 mặt phẳng (SBC) và (ABCD). Do đó, \(\left( {\left( {SBC} \right),\left( {ABCD} \right)} \right) = \left( {AB,SB} \right) = \widehat {SBA} = {45^0}\)
Vì \(SH \bot AB \Rightarrow \widehat {SHB} = {90^0}\). Mà \(\widehat {SBA} = {45^0}\) nên tam giác SHB vuông cân tại H.
Do đó, \(SH = HB = \frac{1}{2}AB = a\)
Thể tích khối chóp S. ABCD là: \(V = \frac{1}{3}SH.{S_{ABCD}} = \frac{1}{3}SH.AB.AD = \frac{1}{3}.a.a.2a = \frac{{2{a^3}}}{3}\)
Chọn D